Exposé sur Pythagore
Intéressée par le sujet au moment de l’introduction du chapitre sur le théorème de Pythagore, une élève de 4e4 a réalisé cet exposé. Vous le retrouverez affiché en salle 111.
Quelques mots sur … PYTHAGORE

Pythagore était un grand philosophe, astronome, musicologue et mathématicien de la Grèce antique. Il est né dans la première moitié du VIe siècle avant J-C, sur l’île de Samos, en Ionie. Il s’installa à Crante en 539 avant J-C. Dans cette ville, il fonda une école de mathématiques et de philosophie et eut denombreux disciples. Les pythagoriciens croient à la toute puissance du nombre qui régit l’univers. C’est de cette croyance que découlent les multiples recherches mathématiques réalisées par l’école dePythagore. Assassiné aux environs de 500 avant J-C, Pythagore est resté célèbre pour avoir démontré une relation dans le triangle rectangle, le fameux théorème de Pythagore étudié en 4 ème : le carré de l’hypoténuse est égal à la somme des carrés des côtés de l’angle droit. On connaissait la propriété de Pythagore bien avant cette époque. On a en effet découvert des tablettes d’argiles gravées par les babyloniens, probablement vers 1 800 avant J-C, donnant les longueurs des côtés de 15 triangles rectangles différents.
Une autre légende raconte comment Pythagore aurait posé les bases de la musique.
Dans une forge, Pythagore écoute résonner une enclume frappée par des marteaux de masses différentes. Il comprend que les différences de résonances de l’enclume répondent à une loi mathématique. Il établit ainsi la gamme musicale qui repose principalement sur les quatre intervalles consonants (unisson, octave, quinte, quarte). Il montre par exemple qu’à partir d’un DO, une corde deux fois plus courte permettrait d’entendre un DO élevé d’une octave, une corde trois fois plus courte donnerait un SOL etc…
Pour Pythagore, la musique est un acte mathématique.

Nous devons aussi à Pythagore, cette propriété connue des élèves de 5ème :
« Dans un triangle, la somme des mesures de ses angles est égale à 180° ».
Pythagore et l’arithmétique (étude des nombres)
On doit aux pythagoriciens d’importants résultats d’arithmétiques comme par exemple :
- Les nombres premiers : ce sont ceux qui n’admettent pas d’autres diviseurs que
1 et eux-mêmes (exemples : 5, 17, 29, etc…)
- Les nombres parfaits : ce sont ceux qui sont égaux à la somme de leurs diviseurs autre que eux même. Par exemple, 6 (qui est égal à 1 + 2+ 3) ou 28 (qui est égal à 1 + 2 + 4 + 7 + 14) sont des nombres parfaits.
- Les nombres amis : m et n sont dits amis lorsque la somme des diviseurs de n (n exclu) vaut m et la somme des diviseurs de m (m exclu) vaut n (exemple 220 et 284).
Table de Pythagore
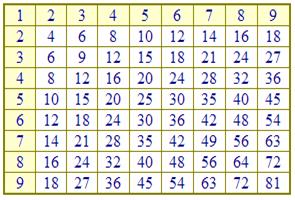
On nomme ainsi un tableau à double entrée indiquant à l'intersection d'une ligne et d'une colonne le résultat d'une opération.
Ci-joint est présentée la table de multiplication attribuée à Pythagore et dont le procédé de formation est le suivant : On écrit les chiffres de 1 à 9 en 1ère ligne et les doubles en seconde ligne. Puis, pour chaque ligne suivante, on écrit la ligne du dessus augmentée de la 1ère. C'est une méthode additive.
On voit se former en 1ère colonne les chiffres de 1 à 9 et le résultat d'une multiplication comme 6 x 7 est lu à l'intersection de la ligne 6 et de la colonne 7 ou vice versa.
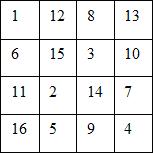
Le carré magique était la curiosité numérique favorite des pythagoriciens. Dans le carré ci-dessous, quel que soit le sens dans lequel vous additionnez une ligne de 4 nombres, vous trouverez toujours un total de 34. Le carré contient une seule fois tous les chiffres de 1 à 16.
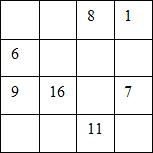
Complétez ce carré magique avec les nombres de 1 à 16 pour que la somme de chaque ligne, chaque colonne et chaque diagonale du carré soit égale à 34.

Pythagore vu par Raphaël.
Théorème de Pythagore
Il existe plus de 300 démonstrations de ce théorème. En voici quelques-unes.
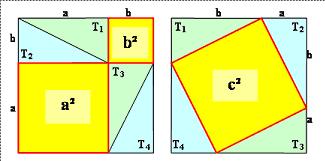
Démonstration faite dans le cahier de leçons
* De chaque grand carré, on retire les quatre triangles:T1 , T2 , T3 , T4 de côtés : a, b et d’hypoténuse: c
* Les surfaces restantes en jaune sont identiques. On a donc : a² + b² = c²
Sans doute la démonstration la plus simple, d'origine indienne.
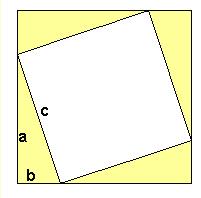
S = (a + b)² = a² + 2ab + b²
S = c² + 4(ab/2) = c² + 2ab
Donc a² + b² = c²
Variante due au mathématicien indien Bhaskara (né vers 1114).
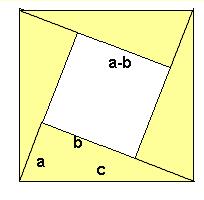
S = 4(ab/2) + (a-b)²
On a donc c² = a² + b²
Élégance de Léonard de Vinci
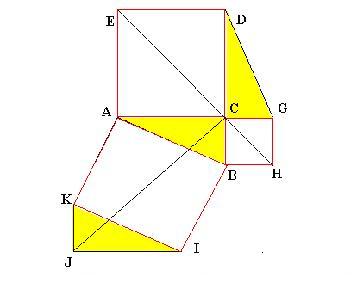
Idée subtile: on duplique le triangle ABC en IJK
On forme ainsi
4 quadrilatères égaux
ABHE = DGHE = AKJC = IBCJ
Or ABHE + DGHE =
grand carré + petit carré + 2 triangles initiaux
et
AKJC + IBCJ =
carré oblique + 2 triangles initiaux