1. Calculer l’énergie des photons associés aux ondes électromagnétiques suivantes :

Onde radio (l = 500 m) ; IR (100 mm) ; rayonnement visible (500 nm) ; UV (100 nm) ; rayonnement X (0,15 nm)

2. Quelle est la précision maximum de la valeur de la quantité de mouvement d’un électron dont la position est déterminée à 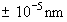? Yaura-t-il des problèmes si la valeur de la quantité de mouvement est

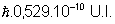
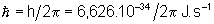
3. La série des raies de Balmer dans le spectre de l’hydrogène correspond à n₁ = 2 dans la relation de Ritz. Calculer l pour les 6 premières raies de la série.

4. L’énergie d’ionisation de l’atome d’hydrogène, à partir de son état fondamental, est de 13,6 eV,

4.1. Quelle est la radiation de plus courte longueur d’onde que peut émettre l’atome d’hydrogène ?

4.2. Donner l’expression de l’énergie caractérisant les différents états énergétiques de l’atome d’hydrogène en fonction du nombre quantique principal n. Calculer l’énergie du niveau caractérisé par n = 4. Quelle est la longueur d’onde des radiations qui peuvent être émises lorsque l’atome se désexcite à partir de ce niveau ?

5. Comparer les spectres d’émission de l’hydrogène et du deutérium 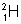, sachant que 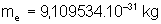, 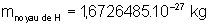et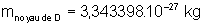

6. Calculer l’énergie d’ionisation (en eV) pour l’atome d’hydrogène à l’état fondamental, grâce aux données suivantes :

Ry = 10967776 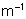; h = 6,626. 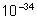J.s ; c = 3. ; .

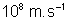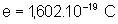7. État excité 3d

On considère l’atome d’hydrogène dans l’état excité 3d.

Quelles sont les transitions d’émission possibles ? Les représenter sur un schéma.

Calculer les longueurs d’onde des photons correspondant à ces transitions.

Quelle est l’énergie d’ionisation de l’atome d’hydrogène dans cet état excité (en eV et en kJ. Mol–1) ?

Données : Énergies propres de l’atome d’hydrogène :

En= – 13,6 / n² (eV), (n entier > 0).

4) Ritz constata que certaines des fréquences correspondantes se déduisent des autres par combinaison linéaires. Vérifier cette relation.

8. Vrai ou faux ?

Identifier les propositions fausses et les rectifier. (O.A. = orbitales atomiques)

8.1. L’énergie de l’électron dans l’atome d’hydrogène ne dépend que du nombre quantique principal n.

8.2. Les O.A. de type s ont la symétrie sphérique.

8.3. Une surface nodale est une surface sur laquelle la fonction d’onde est minimale.

8.4. Les O.A. 2p_x, 2p_y et 2p_z sont de révolution autour des axes de coordonnées.

8.5. He²⁺ est un ion hydrogénoïde.

8.6. Dans Li²⁺, l’énergie des orbitales atomiques ne dépend que du nombre quantique principal n.

8.7. Un atome excité est un atome qui a perdu un électron.

8.8. Le rayon des orbitales atomiques diminue lorsque le nombre quantique principal augmente.

8.9. L’O.A. y_4,1,0 a la symétrie sphérique.

8.10. Les O.A. 3dxy, 3dyz et 3dzx sont de révolution autour des axes de coordonnées.

8.11. L’O.A. y_4,3,3 est une O.A. de type f.

8.12. En émettant un photon (une onde électromagnétique), un atome retourne toujours à l’état fondamental.

8.13. L’énergie d’ionisation de He+ est quatre fois plus grande que celle de l’atome d’hydrogène.

8bis. Ion hydrogénoïde

1) Rappeler la définition d’un ion hydrogénoïde

2) Les valeurs de l’énergie propre de ces systèmes satisfont à la relation : E_n= – E_i / n² où n est un entier strictement positif. Que représente E_i ?

3) Les ions Be⁺ et Li²⁺ sont-ils des systèmes hydrogénoïdes ?

4) Les énergies d’ionisation de He⁺ et Li²⁺ sont respectivement 54,4 eV et 122 eV. Peut-on trouver une relation simple entre leur nombre de charges, leur énergie d’ionisation et celle de l’atome d’hydrogène ?

5) Calculer la valeur de l’énergie propre des quatre premiers niveaux de ces atomes. Les comparer à ceux de l’atome d’hydrogène. Pourquoi peut-on dire que l’électron devient de plus en plus lié à mesure que Z augmente ?

9. Désexcitation

1) Des atomes d’hydrogène initialement à l’état fondamental, sont excités par un rayonnement U.V. de longueur d’onde 97,35 nm. Quel est le nombre quantique principal de l’état ainsi obtenu ?

2) Quelles sont les longueurs d’onde des différentes radiations que peuvent émettre les atomes lorsqu’ils se désexcitent ?

10. Principe de Pauli

Parmi les configurations électroniques suivantes, quelles sont celles qui ne respectent pas le principe d’exclusion de Pauli ?

Que peut-on dire des atomes correspondants ?

1s³2s²2p⁶

1s²2s²2p⁵

1s²2s²2p⁴3s¹3p¹

1s²2s²2p⁶3s²3p⁶3d¹⁰4s²

1s²2s²2p⁶3s²3p⁶3d¹⁴4s²

11. Principe de construction

1) Établir la configuration électronique de l’atome de fluor (Z = 9) à l’état fondamental.

2) Soit un atome de fluor de formule électronique 1s22s22p43s1 ; comparer qualitativement son énergie à celle de l’atome de fluor à l’état fondamental.

12. Règles d’établissement de la configuration électronique

On propose différentes configurations électroniques pour l’atome de nickel (Z = 28) :

1s22s22p63s23p63d104s0 ;

1s22s22p63s23p83d64s2 ;

1s22s22p63s23p63d84s2 ;

1s22s22p63s23p63d64s24p2 ;

Parmi ces configurations :

1) Quelle est celle qui ne respecte pas le principe de Pauli ?

2) Quelle est celle qui représente l’atome de nickel à l’état fondamental ? Préciser, si nécessaire, le nombre d’électrons célibataires.

3) Quelle est celle qui ne comporte aucun électron célibataire ?

4) Classer, par ordre d’énergie croissante, les différentes configurations.

13. Détermination de la configuration électronique

Déterminer la configuration électronique des atomes ou ions suivants dans leur état fondamental :

O (Z= 8) ; Al³⁺(Z = 13) ; Cl^–(Z= 17) ; K (Z= 19) ; Fe (Z = 26) ; Hg (Z = 80).

14. Utilisation de la représentation de Lewis

L’atome d’un élément, X, à identifier a pour représentation de Lewis dans l’état fondamental :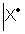

1) Combien d’électrons de valence possède-t-il ?

2) Sachant que leur nombre quantique principal est 2, déterminer le numéro atomique de X et établir la configuration électronique complète de son atome.

3) Identifier X par son nom et son symbole.

15. Noble cœur et configuration électronique

1) Établir la configuration électronique de l’atome de calcium (Z = 20) dans l’état fondamental.

2) Représenter cette configuration à l’aide du cœur correspondant à un gaz noble.

16. Utilisation de la représentation de Lewis

L’atome d’un élément, Y, à identifier a pour représentation de Lewis dans l’état fondamental :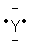

1) Combien d’électrons de valence possède-t-il ?

2) Sachant que leur nombre quantique principal est 3, déterminer le numéro atomique de X et établir la configuration électronique complète de son atome.

3) Identifier Y par son nom et son symbole.

17. Détermination de la représentation de Lewis

1) Déterminer la configuration électronique des atomes ou ions suivants dans leur état fondamental :

S^2– (Z= 16) ; Ca (Z=20) ; Be (Z=4) ; Na+ (Z = l l) ; Cu (Z = 29)

2) En déduire la représentation de Lewis correspondante.

18. Vrai ou faux !

Parmi les propositions suivantes, déterminer celles qui sont erronées et les rectifier.

Dans un atome polyélectronique, la charge effective ressentie par un électron est toujours inférieure à la charge du noyau

L’effet d’écran ressenti par un électron est le même pour tous les électrons de l’atome.

19. Configuration électronique et Tableau périodique

Les réponses aux questions sont à donner sans consulter le Tableau Périodique.

1) Trouver la configuration électronique des éléments suivants :

a) un chalcogène de numéro Z inférieur à 20.

b) un halogène, de même période que le potassium (Z = 19 ).

Classer, en fonction de leur configuration électronique, les espèces chimiques