Etude des molécules
par la méthode de Huckel

Nous nous intéressons aux molécules organiques conjuguées telles que le butadiène ou le benzène. Leur caractéristique principale réside dans le fait qu’ils sont formés uniquement d’atomes de carbone hybridés . L’étude spectroscopique de ces molécules (RX) montre que ces atomes de carbone sont tous coplanaires. Nous nous occuperons donc des orbitales moléculaires formées à partir des orbitales atomiques de chaque carbone perpendiculaires au plan moléculaire, et par conséquent parallèles entre elles.

La thermodynamique montre que l’énergie interne de ces molécules est inférieure à celle attendue pour un ensemble de liaisons p non conjuguées.

1. Principe de la méthode

* il y a autant d’orbitales moléculaires p que d’orbitales atomiques .

* on va séparer l’Hamiltonien total en une somme d’Hamiltoniens uniélectroniques n’opérant que sur un électron à la fois.

* l’énergie propre correspondant à chaque fonction d’onde moléculaire doit être minimale pour toute variation des coefficients dans y , fonction d’onde : c’est la méthode des variations :

2. Cas du radical allyl :

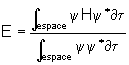
On dispose ici de trois orbitales atomiques sur chaque atome de carbone : j 1 , j 2 , j 3 . Par combinaison linéaire différentes on ne pourra obtenir que trois orbitales moléculaires : y 1 , y 2 , y 3 .

On appellera

Voici les expressions proposées pour chaque orbitale moléculaire :

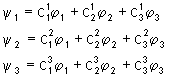
On constate que formellement ces expressions sont semblables. Aussi suffira-t-il de dériver une seule expression par rapport aux trois coefficients .

2.1. Calcul de l’énergie.

avec

2.2. On pose, pour répondre aux exigences de la Thermodynamique :

Nous obtenons trois expressions en dérivant E par c1 ,c2 ,c3 . Soit D le dénominateur de E et N le numérateur.

Pour que ces trois expressions soient nulles quelques soient c_i , il faut et il suffit que le déterminant correspondant soit nul. auparavant, le fait que permet une notable simplification des expressions ci-dessus : (Hij = Hj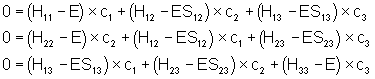i)

(I)

Voici le déterminant qui doit s’annuler, appelé déterminant séculaire :

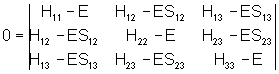
2.3. Approximations de Hückel.

Elles sont valables quel que soit l’hydrocarbure conjugué :

* pour chaque atome de carbone, Hii = a : c’est l’intégrale coulombienne que l’on calcule pour l’atome seul en utilisant les approximations de Slater.

* si i ¹ j , Hij = 0 , sauf si i = j ± 1 (les deux atomes sont adjacents). Dans ce cas, Hij = b : c’est l’intégrale de résonance, ou intégrale de recouvrement.

* Sij = 0 , si i ¹ j .

Le déterminant devient alors :

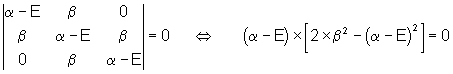
 On constate que chaque ligne correspond à un atome participant à la conjugaison, que l’on attribue la valeur x à l’atome lui-même, la valeur 1 à un atome adjacent, et la valeur 0 à tout autre atome.

Les trois valeurs propres de l’énergie correspondant aux trois fonctions d’onde moléculaires sont les solutions de l’équation ci-dessus :

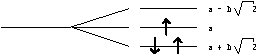On dispose les trois électrons provenant des OA . L’énergie totale des électrons est donc :

Le calcul, identique et simple, fait en considérant le radical totalement indépendant de la double liaison, donne le résultat suivant :

L’énergie de résonance, ou de conjugaison vaut donc E – E’ , soit

Détermination des coefficients ci des 3 orbitales moléculaires.

Il suffit de remplacer dans les équations (I) , E par les 3 valeurs propres successivement. La résolution du système en ci donne les expressions des fonctions d’onde relatives à chaque valeur propre :

a ) E = E1

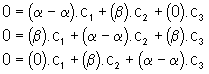
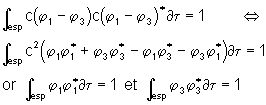
La résolution de ce système donne : c = . La fonction d’onde y 1 correspondante doit être normée, c’est-à-dire que . Ce qui donne :

car les orbitales atomiques sont orthonormées par définition.

On obtient donc et la fonction d’onde y 1 s’écrit :

b ) E = E2

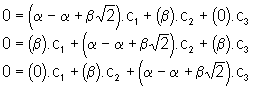
On trouve donc , donc . Le calcul de normalisation donne .

g ) E =E3

Un calcul tout à fait similaire conduit à .

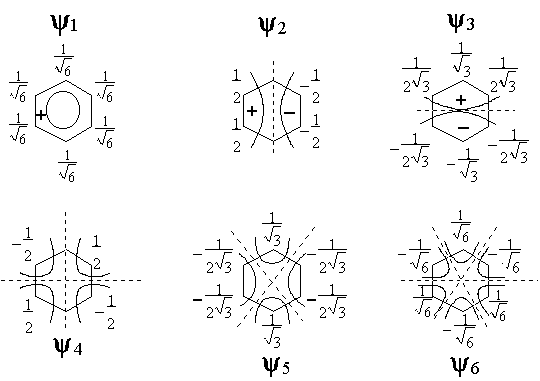
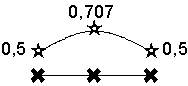On constate donc que la fonction correspondant à la plus basse énergie est positive sur chaque atome de carbone, et donc sur toute la molécule. Graphiquement, on peut dessiner cet état de chose ainsi :

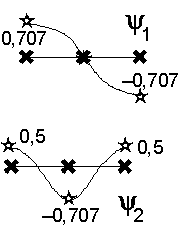
Cette fonction ne présente pas de zéro sur la molécule. Les deux autres fonctions sont représentées ainsi :

est une fonction qui présente un zéro sur un atome de carbone, et aucun zéro entre deux atomes consécutifs : c’est une fonction non liante. Par contre , qui s’annule deux fois sur la molécule et entre chaque atome de carbone, est une fonction antiliante.

Calcul de la densité de charge sur chaque atome :

r est le numéro de l’atome sur lequel on cherche à déterminer la charge, j est l’indice correspondant à chaque orbitale moléculaire, et n est le nombre d’électrons remplissant la orbitale moléculaire.

Pour le radical allyle :

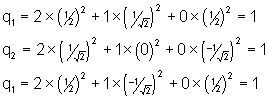
Calcul de l’indice de liaison : il est proportionnel à la densité entre les atomes :

Donc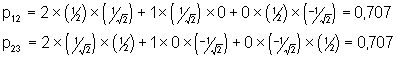

On constate donc que l’indice de liaison p est le même pour les deux liaisons. La vision classique de la délocalisation donnait un indice de 1 pour les deux liaisons (soit 0,5 pour chaque liaison). On constate une augmentation de cet indice dans le modèle de Hückel, ce qui correspond à l’augmentation de l’énergie de chaque liaison due à l’énergie de résonance. Ces mêmes liaisons auront une longueur intermédiaire entre celle d’une liaison simple et celle d’une liaison double.

Indice total de liaison (s + p ) : 1,707. Une formule approchée donne la longueur d’une liaison en fonction de l’indice de liaison p : . Donc ici, l = 0,137 nm.

3. Étude de la molécule de butadiène :

On dispose ici de 4 O.A. . Par combinaisons linéaires on obtiendra quatre orbitales moléculaires p différentes. De même que précédemment on va exprimer E en fonction d’un quadruplet quelconque de coefficients scalaires :

Dérivons par rapport aux et nous obtenons le système de 4 équations suivant :

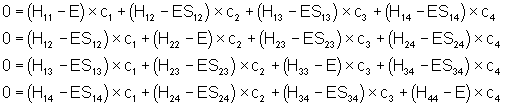
En appliquant les approximations de Hückel, le déterminant séculaire devient :

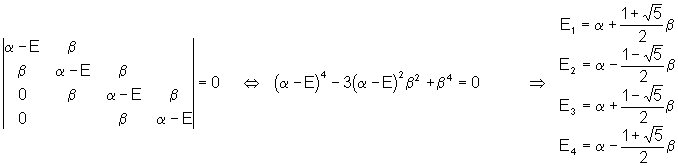
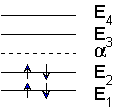
Calcul des coefficients relatifs aux différentes orbitales moléculaires :

u E = E1 : nous obtenons le système suivant :

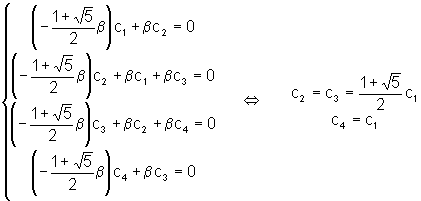
u La normalisation de la fonction d’onde correspondante permet de calculer c₁ :

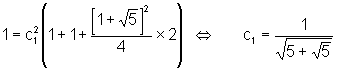
u Le calcul est semblable pour les trois autres valeurs de l’énergie. Les 4 fonctions d’onde s’expriment alors ainsi :

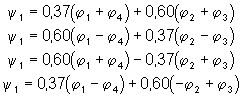
u Représentation des fonctions d’onde :

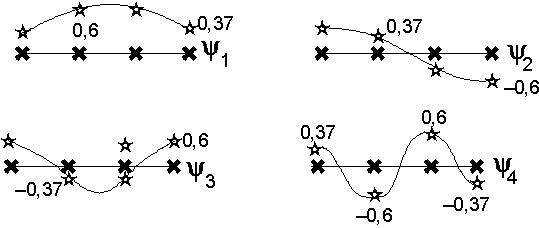
u Calcul de la densité de charge :

u Calcul de l’indice de liaison :

u Le calcul classique, négligeant la conjugaison, aurait donné : deux fonctions d’onde liantes entre 1 et 2 et entre 3 et 4, d’énergie a + b , et deux fonctions d’onde antiliantes sur les mêmes liaisons, d’énergie a – b . L’indice de liaison p vaut alors 1 pour et 0 pour .

On constate donc que l’énergie de conjugaison est, pour le butadiène :

u Longueurs de liaison :

 Plus généralement, les niveaux d’énergie des polyènes conjugués comportant N atomes de carbone peuvent être calculés par la relation de COULSON :

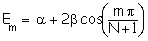
            Les coefficients de l’OA « k » dans les OM « p » de ces polyènes sont les suivants :

 4. Étude des orbitales délocalisées du propènal

                        Le déterminant séculaire appliqué aux 4 atomes, donne :

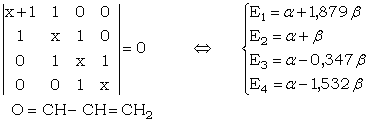
                        Les solutions sont au nombre de 4

                        Cela donne le diagramme énergétique suivant :

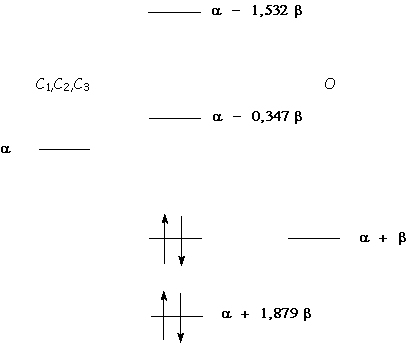
Cela nous donne une énergie électronique pour le système p égale à : 4a + 5,758 b .

Un calcul simple donne l’énergie du sytème p de C=O isolé ; on trouve 2a + 3,236 b. Celle de l’éthène vaut 2a + 2b. L'énergie de résonance du propènal vaut :

E_R = 4a + 5,758b - (2a + 3,236 b + 2a + 2b ) = 0,522b .

On constate d’autre part que la densité électronique est concentrée sur l’atome d’oxygène. Cherchons maintenant l’expression des OM p du propènal :

u E = E₁ : nous obtenons le système suivant :

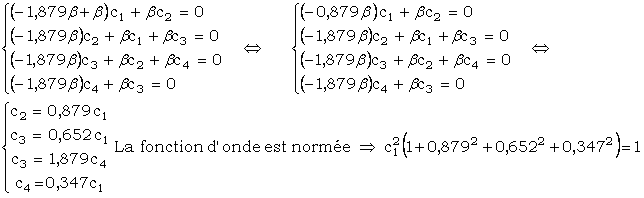
On en déduit :

Faire de même pour les autres OM :

Nous pouvons maintenant déterminer les densités de charges .

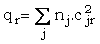
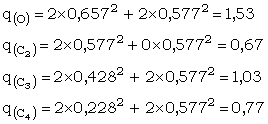
On constate donc que le C le plus électrophile est celui du carbonyle, suivi de près par le carbone en 4 (addition 1,4)

 Les indices de liaison sont les suivants

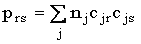
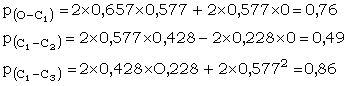
On constate bien l’apparition d’un caractère p pour la liaisn C1 – C2 . De plus l’indice de liaison total est > 2 (2,12), ceci étant une nouvelle preuve du phénomène de résonance.

5. Étude des orbitales délocalisées dans la molécule de benzène.

En calculant le déterminant séculaire des deux précédents systèmes, nous avons pu constater que pour l’atome i relatif au coefficient , le terme correspondant du déterminant était a – E . Pour la même dérivation par , les termes correspondant aux atomes voisins sont égaux à b . Tous les autres termes sont nuls.

Soit la molécule de benzène :

Il y a 6 fonctions d’onde atomiques à combiner et nous obtiendrons 6 fonctions d'onde moléculaires. Pour la première ligne du déterminant, nous aurons donc : car l’atome est voisin de .

u Le déterminant total est donc :

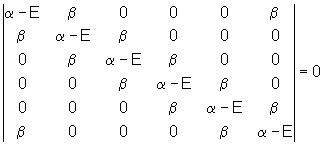
dont le développement donne : . Les solutions en E de cette équation sont au nombre de 6 :

Il y a donc deux niveaux d’énergie dégénérés. L’énergie totale des 6 électrons est donc égale à . L’étude classique (3 doubles liaisons) donne . L’énergie de conjugaison vaut donc 2b .

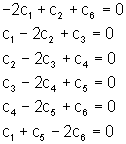u Détermination des fonctions d’onde.

F E = E1 : La seule solution à ce système d’équations est : . La normalisation de la fonction correspondante donne

F E = E2 : La simplification du système des 6 équations obtenues donne le résultat suivant :

Il nous faut donc encore d’autres équations pour résoudre le problème. Nous utiliserons l’équation de normalisation de : (II) . Nous constatons que la première équation a un nombre infini de solutions. Nous allons choisir une valeur simple pour , par exemple , ce qui donne , donc .

donc .

Comme E = E2 est une racine double, il existe une autre fonction d’onde qui a pour énergie propre E2 . Ses coefficients sont régis par les 5 mêmes équations que . L’équation manquante peut être déterminée par le fait que la densité de charge doit être identique sur chaque atome de carbone et égale à 1. Soit les coefficients à rechercher. Nous devons avoir :

u sur :

u sur :

u comme , . On vérifie aisément que la charge de vaut également 1 et que l’équation (II) est vérifiée :

u Par des raisonnements semblables, on montre que les trois autres fonctions d’onde s’expriment de la manière suivante :

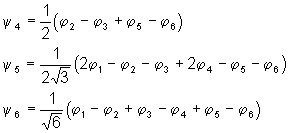
u Le calcul de l’indice de liaison donne 0,67 pour chacune d’entre elles.

u Représentation des fonctions :