L'oxygène est l'élément le plus abondant de la croûte terrestre. La vie des animaux et des hommes en dépend de manière indispensable. L'utilisation industrielle de l'oxygène, récente, devient très importante. Les composés chimiques minéraux les plus importants en contiennent.
1.1. Propriétés physiques.
1.1.1. Isotopes.
Ils sont au nombre de trois principalement : ,
,
. Ces
isotopes peuvent être séparés par distillation fractionnée de l'eau. Les
isotopes rares sont d'une grande utilité en recherche organique par exemple :
a un
spin nucléaire non nul
, ce qui permet de faire des déterminations de
structure par RMN de
.
sert de marqueur dans l'étude de nombreux mécanismes
réactionnels.
1.1.2. Variétés allotropiques, changements d'états.
Il existe deux variétés allotropiques possédant chacune les trois phases : O2 (oxygène) et O2 (ozone). Les températures de changement d'état sont les suivantes : pour O2 , tf = -219°C , te = -183°C ; pour O3 , tf = -193°C , te = -112°C . L'oxygène liquide est bleu, l'ozone bleu-foncé.
1.1.3. Paramagnétisme.
Définition : la susceptibilité paramagnétique électronique se rencontre dans :
- les atomes, les molécules et les défauts cristallins (cf. § sur les métaux de cours) possédant un nombre impair d'électrons, car, dans ce cas, le spin total du système ne peut être nul Citons, par exemple, les atomes libres de sodium ; NO gazeux ; le radical triphényleméthyle.
- les atomes et les ions libres dont une couche
interne est incomplète : les éléments de transition, les terres rares, les
actinides Un grand nombre de ces ions ( ,
,
) sont
paramagnétiques quand ils font partie d'un solide.
- quelques composés ayant un nombre pair d'électrons, dont O2 et les radicaux organiques doubles (carbène à l'état de triplet).
- les métaux.
Ce paramagnétisme se traduit par l'apparition d'un
moment magnétique de spin électronique où
somme des spins
électroniques et G est le rapport gyromagnétique. Soumis à un champ magnétique
variable, l'échantillon paramagnétique est soumis à la force
. En utilisant un
entrefer où H = k(x) , on obtient
.
Soit m la masse de l'échantillon. En appliquant le
principe de la dynamique du point matériel à l'échantillon, on obtient : .
L'équilibre ( = 0), est obtenu pour
. Connaissant H =
k(x), on en déduit le déplacement x de l'échantillon. On préférera une fonction
logarithmique pour H, ce qui donne
, soit
, donc
une variation de x proportionnel à M.
1.1.4. Longueur de liaison.
l = 0,121 nm , proche d'une double liaison.
1.2.1. Abondance.
O est contenu à raison de 47% (en masse), dans la lithosphère ; 89% dans l'hydrosphère ; 21% en volume dans l'atmosphère.
1.2.2. Préparation industrielle.
On utilise la distillation fractionnée de l'air liquide. La température d'ébullition de N2 est de 192°C. Il faudra donc une colonne comportant un nombre élevé de plateaux théoriques L'opération est cependant très rentable, à cause des nombreuses utilisations industrielles de l'oxygène : comburant (fusées, aciéries,…), santé,…
2. Structure de la molécule. (oxygène et ozone)
Nous avons étudié cette structure On constate en étudiant le diagramme des O.M., qu'il y a deux électrons non appariés distribués dans les 2 O.M. antiliantes, d'où le paramagnétisme. La différence faible entre les niveaux p et p* explique la couleur bleue de l'oxygène (transition p p*). On retrouve l'indice de liaison égal à 2.
Sa structure est la suivante: Cette molécule est diamagnétique (spin total nul). La liaison est intermédiaire entre une simple liaison et une double liaison. On peut également représenter la structure de l'ozone grâce aux formes mésomères suivantes
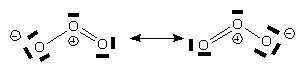
C'est un oxydant énergique.
3. Réactivité de l'oxygène. Étude thermodynamique.
3.1. Ionisation de l'atome d'oxygène
Voici quelques valeurs d'enthalpies pour les diverses réactions d'ionisation :
| - première ionisation de O | |
| - affinité électronique | |
| - affinité électronique | |
| enthalpie de dissociation : | |
On en déduit l'enthalpie de formation des anions :
![]()
Apparemment donc, l'oxygène ionique devrait se
trouver sous la forme ![]() . Or ce n'est pas le cas. Il faut donc étudier les structures
qui comprennent l'anion
. Or ce n'est pas le cas. Il faut donc étudier les structures
qui comprennent l'anion ![]() pour comprendre le phénomène.
pour comprendre le phénomène.
Celui-ci se synthétise lors de la réaction :
Donc l'enthalpie de formation de l'ozone vaut :
On résume grossièrement la tendance de l'oxygène à capter des électrons dans le concept d'électronégativité : elle est élevée pour O (3,5 dans l'échelle de Pauling). C'est pourquoi l'oxygène donne-t-il des composés avec tous les éléments (sauf He, Ne, A). Ce sont les oxydes.
4. Les oxydes.
L'énergie de formation d'un cristal à partir des éléments simples, peut être décrite par un cycle dit de ”BORN - HABER”. Les étapes de ce cycle thermodynamique sont les suivantes (l'exemple utilisé est celui de NaCl) : (voir page suivante).
On constate que la somme des 4 premiers termes est
positive (= 378 kJ.mol-1). Elle correspond à la réaction Na + ½ Cl2 Na+ + Cl- .
Le dernier terme ()
correspond à l'attraction des ions positifs et négatifs les uns sur les autres
C'est l'énergie de réseau ou énergie réticulaire.
|
|
En admettant que l'on travaille sur une mole de NaCl, on aura Nc ions Na+ et Nc ions Cl- . Born a montré que l'énergie réticulaire variait de la manière suivante, en fonction de la distance interatomique, et de Z, la charge mutuelle des ions :
|
|
On y trouve deux termes : le terme d'énergie potentielle coulombienne (le premier), et le terme de répulsion à courte distance La variation de cette somme en fonction de la distance interatomique d est représentée sur le graphique ci-dessous :
On constate un minimum d'énergie (stabilité du cristal maximale) pour une distance d0 appelée distance d'équilibre.
n peut être déterminé expérimentalement par mesure de la compressibilité des cristaux. (n = 9,1 pour NaCl)
La constante A dépend de la structure du cristal, de sa géométrie. On l'obtient en sommant sur tout le cristal, pour un seul ion, les interactions coulombiennes répulsives et attractives qu'il subit. Cette somme est toujours convergente. On obtient un résultat approché en faisant le calcul du potentiel coulombien sur les 4 plus proches voisins.
Voici quelques valeurs :
| Structure |
A |
|
| NaCl |
1,748 |
cubique à faces centrées |
| CsCl |
1,763 |
cubique centré |
| ZnS |
1,638 |
blende |
| CaF2 |
5,039 |
fluorine |
4.2. Géométrie des édifices ioniques vrais
4.2.1. Structure cubique centrée CsCl.
Maille du chlorure de césium
Dans la maille représentée, il y a un ion et un ion
pour que l'anion et le cation
soient en contact, nous devons avoir :
d'autre part,
l'arête du cube ne peut être que supérieure ou égale à deux fois le rayon e
: donc
. Nous en déduisons
le rapport
. Dans ce type de structure,
, car
, ne peut être supérieur à
Exemples :
| 0,133 | 0,181 | 0,196 | 0,219 | ||
| 0,068 | 0,098 | 0,133 | 0,148 | 0,167 |
pour CsCl, le rapport vaut 0,92, pour
CsBr et CsI , il vaut respectivement 0,85 et 0,76.
Elle est égale au rapport du volume occupé dans la
maille par les ions appartenant en propre à la maille sur celui de la maille.
Dans CsCl, il y a un ion positif et un ion négatif. Donc et, puisque
,
. La
compacité C est donc égale à :
Par exemple, pour CsBr, C = 0,694
4.2.2. Structure cubique à faces centrées.
La structure cubique à faces centrées
Dans la maille représentée, il y a 4 ions et 4 ions
. Pour que l'anion et le cation
soient en contact, nous devons avoir :
. Les ions
ne peuvent être en
contact que sur la diagonale d'une face. Donc
. En faisant le
rapport, on obtient :
.
La structure cubique à faces centrées se
retrouvera donc surtout lorsque la condition suivante est réalisée : . Par
exemple : pour NaCl ,
= 0,54 ; pour CaO ,
= 0,714 ; pour MnO ,
=
0,479 . Cependant, KF a la structure cfc, alors que
= 1.
Calcul de la compacité
Il y a 4 ions positifs et 4 ions négatifs par maille. Donc :
, et
soit , ce qui donne
pour C :
Pour MnO par exemple, où = 0,479 ,
C = 0,719
C'est une structure CsCl dans laquelle il manque
un centre sur deux. De même qu'en 4.2.1., . Les oxydes
alcalins ont une structure antifluorine.
4.3. Structures à caractère ionique prépondérant.
Structure blende ZnS.
ZnS existe aussi sous la forme würtzite (voir 4.3.2.)
Dans le cas de la blende, il y a une structure
cubique à faces centrées pour les ions sulfure, et décalée du quart de la
diagonale de la maille pour les ions zinc (dans la moitié des sites
tétraèdriques) : Donc
Et comme pour NaCl, les anions se touchent sur la
diagonale des faces. Donc , soit
. Ce rapport doit
donc être compris entre 0,225 et 0,414 pour que cette structure existe. Ainsi,
pour BeO,
Le calcul de la compacité donne :
avec
,
et
Par exemple, pour BeO , C = 0,748
4.3.2. Structure würtzite (ZnS).
Structure würtzite (ZnS).
Le réseau de chaque type d'ions est hexagonal, et
les deux réseaux sont décalés, de manière à ce que chaque ion ait un
environnement tétraédrique. Calculons en fonction de a :
Dans le tétraèdre régulier ABCD , AD = AB = AC =
BC = BD = CD = a . D étant au centre de ce prisme droit à base triangulaire,
.
Dans le triangle AHD, rectangle en H,
(I). Le triangle
ABH est isocèle, et M, hauteur de ce triangle partant du sommet H, est également
le pied de la médiatrice de AB. Donc 2 AM = AB. Le triangle ABC étant
équilatéral, AH est la bissectrice de l'angle
. Donc
, et
, soit
.Remplaçons les distances AH, HD dans (I) par leur valeur en fonction de a et de
h. Nous trouvons :
soit
.D'autre part, dans le triangle AKH,
, car
soit
Comme toujours, on a la condition suivante sur les
rayons des anions : . On retrouve donc la même condition sur le rapport des rayons
que pour la blende :
.Par exemple, pour ZnO,
Calcul de la compacité.
Le point A appartient à 12 prismes à base
triangulaire. Un prisme sur deux contient un atome de zinc. Il y a donc atome de
zinc en propre à la maille. On trouve de même 1 atome de soufre en propre à la
maille. Le volume de ces atomes vaut :
. Le volume de la
maille vaut
. Soit
. Ou encore
et, en tenant
compte de
,
Nous en déduisons
.Pour ZnO, nous
trouvons C = 0,53.
4.3.3. Structure rutile TiO2 , SnO2 .
Les atomes métalliques sont disposés au sommet d'un parallélépipède rectangle, ainsi qu'en son centre ; les atomes d'oxygène sont disposés au sommet d'un octaèdre régulier centré sur l'atome central, et la distance Ti-O y vaut le tiers de la diagonale du rectangle :
4.3.4. Structure Trioxyde de Rhénium ReO3
4.3.5. Structures lamellaires.
Ici les coordinences sont faibles (4 ou 2), la liaison est donc plus localisée, donc plus covalente. Ce sont des lamelles constituées par un empilement de deux couches de cations entourant une couche double d'anions.
Ils possèdent la
formule
(
par exemple), avec un cation divalent, un cation tétravalent et
un anion divalent, ou bien, comme dans
, les valences
moitié : Les gros cations
, forment une structure cubique simple, les anions
occupant les faces de ce cube, et le petit cation au centre. Si l'on place les
petits cations aux sommets d'un cube, on obtient la deuxième figure qui montre
bien la correspondance avec
. La structure a un caractère covalent marqué.
Ceux-ci par contre sont parfaitement
ioniques, de formule
,soit :
. L'oxygène occupe les sommets d'une maille cubique à
faces centrées ; dans un spinelle direct, le premier cation (A) occupe
des sites
tétraèdriques , les deux autres cations (B) la moitié des sites octaèdriques.
Dans un spinelle inverse, le cation A et un
des cations B occupent la moitié des sites octaèdriques, le dernier cation B
occupant des sites
tétraèdriques.
Les spinelles 4-2 sont tous inverses, par exemple
ou
mieux
.
Les ”aluminates”, ”cobaltates”, etc.… sont directs
: ,
.
La magnétite est un spinelle
inverse :
4.5. Oxydes covalents polymérisés.
Ce sont essentiellement les silicates et la
silice, ainsi que le dioxyde de sélénium , qui est formé
d'une chaîne linéaire.
4.6. Oxydes covalents non polymérisés.
Ces oxydes possèdent tous de basses températures d'ébullition (masse molaire faible) et, dans le cas des métaux de transition, n'apparaissent que pour les degrés d'oxydation élevés. Voici quelques exemples :
, dont les structures sont bien connues. Il existe
quelques oxydes radicalaires stables :
(pyramidal). Les
oxydes de phosphore et de soufre sont des tétramères ou des trimères.
est formé d'un tétraèdre d'oxygènes entourant
l'osmium. Sa température de fusion est donc basse : 41°C.
5. Stabilité thermique des oxydes. Diagramme d'Ellingham.
5.1. Enthalpie libre des réactions d'oxydation.
La définition de la variation d'enthalpie libre G est la suivante :
Généralement, H et S dépendent de la température.
Mais cette variation est minime au regard du terme T.S figurant dans
l'expression précédente. Aussi Ellingham a-t-il proposé d'étudier la variation
d'enthalpie libre de formation des oxydes (ainsi que celle des chlorures), en
admettant que H et S sont indépendant de T. Ceci est d'autant plus vrai pour les
enthalpies libres de formation des oxydes solides. Cette approximation sera dénommée
”Approximation d'Ellingham”.
|
|
| |
| C (s) |
/ |
5,68 |
| O2 (g) |
/ |
204,80 |
| CO2 (g) |
-393,13 |
213,43 |
| CO (g) |
-110,44 |
197,71 |
| H2 (g) |
/ |
130,46 |
| H2O (l) |
-285,20 |
69,90 |
| Ni (s) |
/ |
29,9 |
| NiO (s) |
-239,7 |
38,0 |
Le diagramme correspondant, comportant les
segments de droite relatifs à la formation de ces oxydes consommant une mole
d'oxygène, sera nommé ”Diagramme d'Ellingham”.
Traçons les droites correspondantes pour , grâce
aux données suivantes :
On donne également l'enthalpie de fusion du Nickel
à 1453 K : et l'enthalpie de vaporisation de l'eau à 373 K :
Déterminons tout d'abord l'équation de la droite
pour
les réactions de synthèse de CO et de CO2 :
Voici donc les expressions :
On peut vérifier que ces 3 droites sont concourantes au point
Exprimons maintenant la variation de l'enthalpie libre de formation de l'eau liquide :
Cette expression est valable de 273 K à 373 K. Au delà, la variation d'entropie de la réaction est différente, car l'eau est vaporisée.
Établissons à 373 K un cycle thermodynamique permettant d'exprimer l'expression des fonctions d'état envisagées ici (ce diagramme est valable pour H, S et G) :
Donc, pour la réaction :
comme nous travaillons dans l'approximation d'Ellingham,
et donc :
La variation d'entropie molaire de cette réaction
doit rester constante au dessus de 373 K, et donc .
Or avec
, soit :
Donc
Et
Terminons par les droites relatives à la formation de NiO :
Au dessous de 1453 K, on trouve
On peut établir un cycle thermodynamique semblable au précédent pour déterminer l'enthalpie libre de la réaction quand le nickel est liquide :
De la même manière que précédemment, on trouve :
ou encore :
Soit :
De même,
Et
Il ne nous reste plus qu'à tracer le diagramme d'Ellingham pour ces oxydes, avant de tracer un diagramme plus complet.
Diagramme d'Ellingham
complet (!)
Les métaux, dont la droite représentative pour la formation des oxydes correspondants est au dessous de celle des oxydes qu'ils ont à réduire, pourront le faire, si l'on exclut l'inertie cinétique possible de la réaction.
Voici quelques exemples parmi les plus connus :
l'aluminothermie, pour MnO , ; la calciothermie pour
; la
magnésiothermie pour
. L'utilisation du carbone à haute température est
théoriquement la meilleure façon de réduire tous les oxydes. Or cela n'est
vraiment mis en œuvre que dans la sidérurgie, car, la plupart du temps, il y
essentiellement formation de carbures, tels que les carbures de calcium et
d'aluminium :
5.2. Étude de la stabilité des oxydes en fonction des données structurales et électroniques.
La première constatation est celle de la diminution générale de l'enthalpie de formation au fur et à mesure de la diminution du caractère ionique des oxydes : prenons l'exemple des oxydes de manganèse :
| -380 | -318 | -263 | -105 |
est donné en
.
Le caractère covalent augmente de MnO à .
L'on peut ainsi voir que le caractère covalent augmente en passant des oxydes alcalino-terreux aux oxydes de métaux nobles :
| MO | Enthalpie de formation | contribution ionique | contribution covalente | MO | Enthalpie de formation | contribution ionique | contribution covalente |
| CaO | -635 | -635 | 0 | FeO | -263 | -190 | -73 |
| TiO | -518 | -500 | -18 | CoO | -238 | -150 | -88 |
| VO | -439 | -400 | -39 | NiO | -234 | -145 | -89 |
| MnO | -380 | -320 | -60 | CuO | -146 | -40 | -106 |
| cation | |||
| rayon ionique (nm) | 0,100 | 0,116 | 0,136 |
| enthalpie de formation | -635 | -581 | -552 |
On constate donc que CaO est le plus stable
(structure NaCl), avec , donc inférieur à 0,732 . Par contre, ce même rapport
vaut 0,97 pour BaO (structure NaCl) , donc dans une zone de stabilité plus
faible.
En règle générale, les stabilités des oxydes ioniques d'une même colonne diminuent avec l'augmentation de la taille du cation, donc en descendant dans la classification.
En ce qui concerne les oxydes peu ou pas ioniques,
l'évolution de la stabilité est beaucoup plus aléatoire. On peut simplement dire
que les éléments possédant des OA d d'énergie voisine des OA de valence
auront des oxydes plus stables. Par exemple, les enthalpies de formation de et de
sont
respectivement égales à +80 et -310
.
Enfin, tous les oxydes de degré d'oxydation élevé, qui ont pratiquement tous une structure covalente, sont de plus en plus stables au fur et à mesure que l'on descend dans une colonne. c'est tout simplement dû à l'augmentation de caractère ionique de la liaison :
| enthalpie de formation | -310 | -318 | -380 | -401 |
5.3. Étude de l'évolution des températures de changement d'état des oxydes.
Il faut distinguer entre les oxydes moléculaires ou polymérisés (qu'ils soient covalents, semi-ioniques ou ioniques). Les températures de changement d'état des oxydes covalents dépendent de leur masse molaire, et n'évoluent pas en rapport avec leur stabilité :
|
|
| |
|
-79°C |
45°C | |
| enthalpie de
formation
|
-196 |
-142 |
Par contre, dans les structures polymérisées, la rupture des liaisons, favorisée par une stabilité faible de l'oxyde, entraîne un changement d'état. Aussi ces températures évoluent-elles alors de la même manière que la stabilité :
|
| ||
| Tf |
2600°C |
650°C |
|
SrO |
| |
| Tf |
2400°C |
1500°C |
|
BaO |
| |
| Tf |
1950°C |
1900°C |
5.4. Peroxydes et superoxydes.
On remarque que l'action de l'oxygène sur les
métaux alcalins donne ,
,
et
principalement. En effet la stabilité des cristaux de type
antifluorine est d'autant plus faible que la taille des cations est importante.
C'est ainsi que les structures les plus stables sont celles où l'anion devient
plus gros, où bien celles où la structure n'est plus antifluorine, mais
semblable à NaCl . Ceci est obtenu en utilisant
à la place de
. L'anion
étant plus gros, la structure de
est plus stable que
celle de
, toutes deux étant antifluorine. Pour
, l'anion est
, ce qui
donne une structure de type ”chlorure de sodium” plus compatible avec les
tailles relatives de
et de
.
6. L'oxygène et les oxydes en solution aqueuse.
La demi-réaction donnant lieu à la réduction de
est
la suivante :
Théoriquement donc, est un bon oxydant.
Mais au niveau d'une électrode métallique ou en carbone, la présence d'oxygène
dans l'eau ne se traduira pas nécessairement par une attaque importante, car le
métal peut absorber le gaz oxygène sans qu'il y ait réaction. Pour que celle-ci
ait lieu, il faut que le potentiel de cette partie métallique permette de passer
outre cette barrière supplémentaire, créée par le gaz adsorbé.
Par exemple, sur une électrode de fer, le
potentiel normal de réduction de à intensité nulle
est de 1,229 V. Si le fer n'adsorbait pas l'oxygène, l'existence d'une certaine
résistance au passage des électrons dans le métal et au passage des ions dans
l'électrolyte qui baigne l'électrode métallique se traduit par une chute ohmique
lorsque l'intensité de la réduction augmente (il est rappelé que l'intensité I
est égale à :
, soit proportionnelle à la vitesse v de la réaction, car le
nombre d'électrons donnés par la cathode est :
, soit
).
Le tracé de la courbe intensité - potentiel de la
réduction de dans le
cas où il n'y a pas d'absorption est donc le suivant :
En réalité, la réduction de ne pourra se faire
sur le fer que si l'on a abaissé le potentiel de 1 V environ. On appelle cet
abaissement la surtension de
sur le fer (Nous verrons tout à l'heure ce qu'il en
est de l'oxydation de l'eau) . Voici le diagramme précédent modifié et donc plus
proche de la réalité :
Pour que l'oxygène soit réellement réduit, il
faudra que le potentiel de l'électrode soit inférieur à 0,3 V. C'est ainsi que
aura
beaucoup de mal à réduire
sur du fer (potentiel rédox du couple
).
L'oxydation de l'eau sur une électrode en fer présente la même difficulté, car il faudra cette fois-ci augmenter le potentiel de l'électrode d'un volt pour avoir dégagement de gaz. On obtient le diagramme suivant :
Donc, sur du fer, le chlore ne pourra oxyder l'eau
(potentiel rédox du couple , qui ne présente pas de surtension).
Cette surtension varie en fonction de l'électrode
sur laquelle se fait la réduction de ou l'oxydation de
.
Ainsi, sur le platine platiné, elle est de l'ordre de 0,37 V ; sur le carbone,
elle vaut 1,6 V.
Étudions par exemple les vitesses relatives de
l'oxydation du fer métallique par et par
grâce à
ce type de diagramme :
Quel va être le potentiel de fonctionnement du
système ? Celui pour lequel le nombre d'électrons donnés par les réducteurs (ici
Fe) est égal au nombre d'électrons reçus par les oxydants (ici et
).
On voit que ceci est réalisé vers 0,5 V, soit lors de l'oxydation par le chlore, car pour ce potentiel, l'oxygène n'est pas capable de capturer des électrons. Par contre, pour un potentiel de l'ordre de -0,1 V, la somme des intensités anodiques (de réduction des oxydants) est largement supérieure à la somme des intensités cathodiques (d'oxydation des réducteurs), et donc le système est instable et ne peut exister en l'état.
Notons que ce modèle est encore approché car il ne tient pas compte de la limitation des intensités par la mobilité des ions en solution. Ainsi, le diagramme correct pourrait avoir l'allure suivante :
6.2. Les oxydes en solution aqueuse.
Ce sont les oxydes fortement ioniques (alcalins, alcalino-terreux, terres rares + scandium et yttrium, ainsi que les oxydes de degré d'oxydation inférieur des métaux de transition).
Ex :
Certains de ces oxydes sont cependant insolubles
dans l'eau (caractère covalent plus marqué : MO des métaux de transition tels
que FeO ou surtout CuO). Il est généralement nécessaire, pour solubiliser ces
oxydes, de se placer dans un milieu plus complexant () ou plus acide :
Ce sont les oxydes covalents (oxydes d'halogènes,
de chalcogènes [S, Se, Te], d'azote, de phosphore, ceux des métaux de transition
possédant le degré d'oxydation maximum : .
L'atome central est fortement électrophile et va
dissocier en capturant
et en libérant
. Voici quelques
exemples :
, oxyde acide polymérisé, est insoluble dans l'eau
(énergie de cohésion très grande), mais est soluble en milieu basique fort pour
donner des silicates, ou en milieu fluorure pour donner des fluorosilicates très
stables (voir cours sur le silicium).
Ces oxydes ont des propriétés intermédiaires : en général insolubles à pH = 7 , mais solubles en milieu acide pour donner le cation solvaté, et en milieu basique pour donner des anions oxygénés. Exemple :
Les limitations cinétiques rendent ces oxydes
totalement insolubles à température ordinaire : CO , NO (radical) et .