1. Phénomène de la R.M.N. : présentation sommaire.
1.1. Moment cinétique d’un noyau atomique.
Le noyau de certains atomes se caractérise par
l’existence d’un moment cinétique ![]() . L’existence
d’un moment cinétique pour le noyau rend celui-ci semblable à une charge
électrique en rotation et lui confère en quelque sorte les caractéristiques d’un
petit solénoïde.
. L’existence
d’un moment cinétique pour le noyau rend celui-ci semblable à une charge
électrique en rotation et lui confère en quelque sorte les caractéristiques d’un
petit solénoïde.
1.2. Moment magnétique du noyau atomique.
Il en résulte pour le noyau un moment magnétique
![]() proportionnel à
proportionnel à ![]() :
: ![]() où g , le rapport gyromagnétique, est une constante
caractéristique du noyau considéré.
où g , le rapport gyromagnétique, est une constante
caractéristique du noyau considéré.
1.3. Énergie interne d’un noyau atomique plongé dans un champ magnétique.
Placé dans un champ magnétique ![]() , un aimant
de moment magnétique
, un aimant
de moment magnétique ![]() acquiert une énergie potentielle supplémentaire Es
donnée par la relation :
acquiert une énergie potentielle supplémentaire Es
donnée par la relation : ![]() , soit encore :
, soit encore : ![]() (I).
(I).
1.4. Quantification de la projection de
![]() sur
sur ![]() .
.
On montre en mécanique ondulatoire que la
projection de ![]() sur
sur ![]() ne
peut prendre que des valeurs discrètes, dont l’unité de quantification est
ne
peut prendre que des valeurs discrètes, dont l’unité de quantification est ![]() .
Ainsi, cette projection, notée
.
Ainsi, cette projection, notée ![]() , ne peut
prendre que les valeurs suivantes :
, ne peut
prendre que les valeurs suivantes : ![]() , où I est le
nombre quantique de spin du noyau (suivant le noyau, I peut prendre les valeurs
0 , ½ , 1 ,
, où I est le
nombre quantique de spin du noyau (suivant le noyau, I peut prendre les valeurs
0 , ½ , 1 , ![]() ,
2 ...) et
,
2 ...) et ![]() est la constante de Planck divisée par 2p .
est la constante de Planck divisée par 2p .
Voici quelques valeurs de I pour divers noyaux :
|
1H |
2H |
12C |
13C |
14N |
15N |
16O |
17O |
19F |
31P |
|
½ |
1 |
0 |
½ |
1 |
½ |
0 |
|
½ |
½ |
Tableau 1
Ainsi, ![]() pourra prendre
les valeurs h , 0 et –h pour le deutérium 2H. Dans le cas du proton
1H et du carbone 13 13C ,
pourra prendre
les valeurs h , 0 et –h pour le deutérium 2H. Dans le cas du proton
1H et du carbone 13 13C , ![]() sera égal soit à +½h , soit à
–½h .
sera égal soit à +½h , soit à
–½h .
1.5. Cas du proton : niveaux d’énergie apparaissant dans le noyau.
D’après le §1.4. , la relation (I) devient : 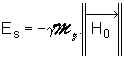 . L’énergie potentielle d’un noyau d’hydrogène en
l’absence de champ magnétique extérieur étant U , ce noyau va pouvoir exister
dans H0 sous deux énergies différentes :
. L’énergie potentielle d’un noyau d’hydrogène en
l’absence de champ magnétique extérieur étant U , ce noyau va pouvoir exister
dans H0 sous deux énergies différentes :
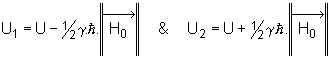
1.6. Transition entre ces niveaux d’énergie.
Le nombre d’atomes d’hydrogène dans chaque état
énergétique est donné par la relation de Boltzmann : ![]() , soit donc
un nombre d’atomes dans l’état U1 bien plus important que ceux
existant dans l’état U2 . Si l’on soumet ce proton, plongé dans un
champ magnétique, à un champ électromagnétique adéquat, il sera possible de
provoquer la transition d’un très grand nombre de noyaux de U1 à
U2 , transition qui sera donc facilement décelable grâce à la baisse
d’intensité importante de l’onde électromagnétique ayant traversé la substance
contenant le proton étudié.
, soit donc
un nombre d’atomes dans l’état U1 bien plus important que ceux
existant dans l’état U2 . Si l’on soumet ce proton, plongé dans un
champ magnétique, à un champ électromagnétique adéquat, il sera possible de
provoquer la transition d’un très grand nombre de noyaux de U1 à
U2 , transition qui sera donc facilement décelable grâce à la baisse
d’intensité importante de l’onde électromagnétique ayant traversé la substance
contenant le proton étudié.
Cette onde électromagnétique aura une fréquence qui suit la relation d’Einstein :
![]()
Cette relation est la relation fondamentale de la RMN.
Exemples : expérimentalement, on constate que, placés dans un champ magnétique de l’ordre de 1,4 T (Tesla), les protons absorbent l’énergie électromagnétique vers 60.106 Hz (fréquence radio). Placés dans le même champ, les noyaux du carbone 13 (13C) absorbent vers 15.106 Hz. Les noyaux de fluor 19 (19F) absorbent vers 56.106 Hz .
2.1. Phénomène du déplacement chimique.
Lorsque l’atome d’hydrogène est engagé dans une liaison, le champ magnétique régnant au niveau du noyau est différent du champ magnétique appliqué H0 . On peut, en effet, considérer que les électrons de liaison forment un écran autour du noyau, écran qui se manifeste par l’apparition d’un champ local DH0 opposé au champ H0 et proportionnel à ce champ : DH0 = – sH0 . La constante de proportionnalité s , appelée constante d’écran, est indépendante du champ appliqué H0 . Elle est fonction de l’environnement chimique du noyau, donc fonction de sa nature chimique.
Pour un proton caractérisé par une constante d’écran s , la fréquence de retournement de spin de ce proton vaut :
![]()
Il résulte de ce phénomène que placés dans un champ magnétique H0 , les divers protons d’une molécule organique absorberont l’énergie à des fréquences différentes qui seront fonction des constantes d’écran correspondantes, donc de l’environnement électronique c’est-à-dire de la nature chimique des protons présents. L’analyse de ce « déplacement chimique » des fréquences d’absorption fournira des renseignements précieux sur la structure des molécules organiques.
Il est à remarquer que les constantes d’écran sont
très faibles de l’ordre de quelques millionièmes. Cependant, le pouvoir de
résolution des spectrographes RMN est remarquablement élevé (environ ![]() Hz
pour un appareil fonctionnant à 60 MHz). cela permet, en fait, d’apprécier des
variations de s de l’ordre de
Hz
pour un appareil fonctionnant à 60 MHz). cela permet, en fait, d’apprécier des
variations de s de l’ordre de ![]() .
.
La différence de fréquence d’absorption pour le
retournement de spin des protons du dichlorométhane ![]() et du
trichlorométhane
et du
trichlorométhane ![]() vaut 118,2 Hz, ce qui correspond à une différence
vaut 118,2 Hz, ce qui correspond à une différence ![]() qui est grande devant le pouvoir de résolution de l’appareil et par suite
facilement mesurable.
qui est grande devant le pouvoir de résolution de l’appareil et par suite
facilement mesurable.
2.2. Mesure de déplacement chimique.
La fréquence d’absorption d’un proton caractérisé
par une constante d’écran s est proportionnelle au champ magnétique appliqué. Il
n’est donc pas commode de repérer le déplacement chimique en fréquence puisque
ce repère dépend du champ utilisé, donc de l’appareil. Aussi repère-t-on
pratiquement les signaux de composé étudié par rapport au signal d’un composé de
référence qui est généralement le tétraméthylsilane ![]() . Le
tétraméthylsilane (ou TMS) a été choisi pour sa volatilité (
. Le
tétraméthylsilane (ou TMS) a été choisi pour sa volatilité (![]() ), son inertie
chimique, et une constante d’écran très élevée : il n’existe que très peu de
composés organiques dans lesquels des hydrogènes présentent des s supérieurs.
), son inertie
chimique, et une constante d’écran très élevée : il n’existe que très peu de
composés organiques dans lesquels des hydrogènes présentent des s supérieurs.
Le déplacement chimique (mesuré en fréquence) du signal d’un proton par rapport au TMS est donné par :
![]()
Pour faire disparaître le terme H0 on
divise les deux membres de cette relation par ![]() , ce qui conduit à une
grandeur notée d, indépendante du champ H0 appliqué :
, ce qui conduit à une
grandeur notée d, indépendante du champ H0 appliqué :
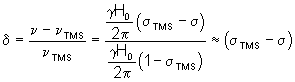
(On peut négliger ![]() devant 1 ,
car il est de l’ordre du cent millième).
devant 1 ,
car il est de l’ordre du cent millième).
Remarques importantes :
a) les constantes s sont de l’ordre du millionième et il en est évidemment de même de leurs différences. Le déplacement chimique d sera donc généralement exprimé en « parties par million» (ppm)
b) Fréquence d’absorption et champ magnétique sont liés par une relation linéaire. Il est donc possible expérimentalement d’enregistrer les spectres RMN en opérant indifféremment à champ constant en faisant varier la fréquence, ou bien à fréquence constante en faisant varier le champ. Pratiquement la deuxième solution est, pour des raisons qui tiennent à l’appareillage, la plus fréquemment retenue. Les spectres sont alors présentés dans la forme ci-dessous :
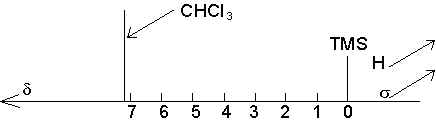
Le champ est croissant de la gauche vers la droite. Les signaux apparaissant à droite dans le spectre correspondent donc aux s les plus élevés.
Le déplacement chimique va croissant de la droite vers la gauche.
La relation entre le déplacement mesuré en Hz et
le déplacement chimique est évidente : ![]() soit, pour
notre appareil à 60 MHz :
soit, pour
notre appareil à 60 MHz :
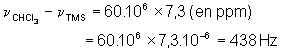
Et plus généralement : « déplacement en Hz » = d (ppm) ´ A (MHz) , où A est la fréquence de fonctionnement du spectrographe.
2.3. Facteurs agissant sur le déplacement chimique.
Voici trois tables donnant les plages déplacements chimiques correspondant à divers types de protons :
table 1
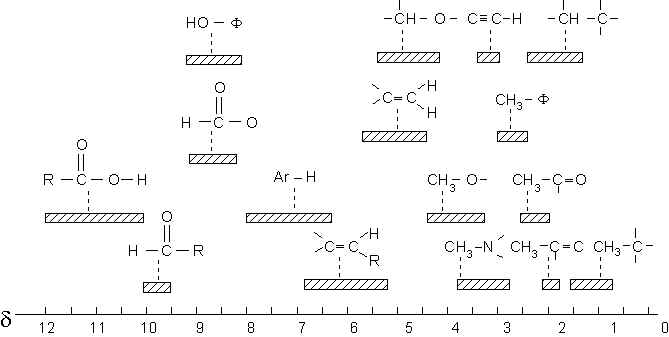
table 2
| CH3 | CH2 | CH | |||
|
proton |
d |
proton |
d |
proton |
d |
| CH3 – C | 0,9 | – C – CH2 – C | 1,3 | – C – CH – C | 1,5 |
|
(cyclique) |
1,5 | (en tête de pont) | 2,2 | ||
| CH3 – C – C= | 1,1 | – C–CH2 – C – C=C | 1,7 | ||
| CH3 – C – O | 1,4 | – C – CH2 – C – O | 1,9 |
– C – CH – C – O |
2 |
| CH3 – C=C | 1,6 | – C – CH2 – C=C | 2,3 | ||
| CH3 – Ar | 2,3 | – C – CH2 – Ar | 2,7 | – C – CH – Ar | 3 |
| CH3 – CO – R | 2,2 | – C – CH2 – CO –R | 2,4 |
– C – CH – CO – R |
2,7 |
| CH3 – CO – Ar | 2,6 | ||||
| CH3 – CO – OR | 2,0 | – C – CH2–CO–OR | 2,3 | ||
| CH3 – CO – OAr | 2,4 | ||||
| CH3 – CO – NR | 2,0 | ||||
| CH3 – OR | 3,3 | – C – CH2 – OR | 3,4 | – C – CH – OR | 3,7 |
| CH3 – OH | 3,4 | – C – CH2 – OH | 3,6 | – C – CH – OH | 3,9 |
| CH3 – O – Ar | 3,8 | – C – CH2 – O – Ar | 4,3 | ||
| CH3 – O – CO – R | 3,7 | –C–CH2 –O–CO–R | 4,1 | –C–CH –O–CO– R | 4,8 |
|
CH3 – N – |
2,3 | – C – CH2 – N – | 2,5 | – C – CH – N – | 2,8 |
| CH3 – N+ | 3,3 | ||||
| CH3 – S – | 2,1 | – C – CH2 – S – | 2,4 | ||
| CH3 – C – NO2 |
1,6 |
C–CH2 – NO2 |
4,4 |
C–CH – NO2 |
4,7 |
| C–CH2 – C – NO2 | 2,1 | ||||
|
CH3 – C=C – CO |
2,0 |
–C–CH2 –C=C–CO |
2,4 |
||
|
C = C(CH3) – CO |
1,8 |
– C=C(CH3) – CO |
2,4 |
||
 |
5,9 |
||||
|
CH3 – Cl |
3,0 |
– C – CH2 – Cl |
3,4 |
– C – CH – Cl |
4,0 |
|
CH3 – C – Cl |
1,5 |
– C – CH2 – C – Cl |
1,7 |
– C – CH – C – Cl |
1,6 |
|
CH3 – Br |
2,7 |
– C – CH2 – Br |
3,3 |
– C – CH – Br |
3,6 |
|
CH3 – C – Br |
1,7 |
– C – CH2 – C – Br |
1,7 |
– C – CH – C – Br |
1,7 |
|
CH3 – I |
2,2 |
– C – CH2 – I |
3,1 |
– C – CH – I |
4,2 |
|
CH3 – C – I |
1,9 |
– C – CH2 – C – I |
1,8 |
– C – CH – C – I |
1,9 |
| CH3 – CN | 2,0 | – C – CH2 – CN |
2,3 |
– C – CH – CN |
2,7 |
|
– CO – CH2 – Ar |
3,8 | ||||
|
0,3 |
0,7 | ||||
| 2,6 | 3,1 | ||||
Table 2
 |
4,6 |
|
7,2 |
| – C
= CH2
– C = CH – – C = CH – (cyclique) R – C º C – H Ar – H |
4,3 5,1 5,3 3,1 9,0 - 7,0
|
– CO – OH C = C – OH R – OH Ar – OH Ar – OH (liaison H intramoléculaire)
|
8,5 - 13
11 - 17 0 7 ~ 5,5 4,2 ~ 7,1 10 - 14 |
| – C = CH –
CO
– CH = C – CO |
5,9
6,8 |
R – NH –
Ar – NH – |
0,6 ~ 5
2,9 ~ 4,7 |
| R – CHO
Ar – CHO H – CO – O – H – CO – N – |
9,9
9,9 8,0 8,0 |
R – CO – NH
–
CHCl3 H2O |
5 ~ 8
7,2 ~ 5 |
Il existe quelques formules empiriques qui permettent de retrouver les déplacements chimiques des protons des groupements méthylène et des protons éthyléniques :
a) Règles de Shoolery qui concernent X — CH2 — Y
![]()
Tableau des incréments s
| –CH3 | –C=C | –CºC | –F | –CF2 | CF3 |
| 0,47 | 1,32 | 1,44 | 1,85 | 1,21 | 1,14 |
| –Cl | –Br | –I | –OH | –OR | –OF |
| 2,53 | 2,33 | 1,82 | 2,56 | 2,36 | 3,23 |
| –O–CO–R | –CO–R | –CO–F | –CO–OR | –CO–NR2 | –CºN |
| 3,13 | 1,70 | 1,84 | 1,55 | 1,59 | 1,70 |
| –NR2 | –NH–CO–R | –N3 | –SR | –OSO2R | |
| 1,57 | 2,27 | 1,97 | 1,64 | 3,13 |
b) Règles de TOBEY. PASCUAL, MEYER, SIMON
Dans l'application de cette règle, chaque substituant a une constante différente suivant son orientation cis, trans ou gem par rapport à l'hydrogène dont on calcule le déplacement chimiqued = 5,28 + sgem + scis + strans
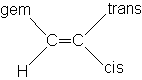
| Groupe | sgem | scis | strans | Groupe | sgem | scis | strans |
| H | 0 | 0 | 0 | -CO2H | 1.00 | 1.35 | 0.74 |
| Alkyl | 0.44 | - 0.26 | - 0.29 | -CO2H (conj.) | 0.69 | 0.97 | 0.39 |
| (CH3) | (0.44) | (- 0.32) | (- 0.34) | -CO2R | 0.84 | 1.15 | 0.56 |
| Cycloalkyl | 0.71 | - 0.33 | - 0.30 | -CO2R (R conj.) | 0.68 | 1.02 | 0.33 |
| -CH2-O- | 0.67 | - 0.02 | - 0.07 | -CHO | 1.03 | 0.97 | 1.21 |
| -CH2-S- | 0.53 | - 0.15 | - 0.15 | -CO-N | 1.37 | 0.93 | 0.35 |
| -CH2-Cl, -CH2-Br | 0.72 | 0.12 | 0.07 | -CO-Cl | 1.10 | 1.41 | 0.99 |
| -CH2-N | 0.66 | - 0.05 | - 0.23 | -OR (R aliph.) | 1.18 | - 1.06 | - 1.29 |
| -CºC- | 0.50 | 0.35 | 0.10 | -OR (R conj.) | 1.14 | - 0.65 | - 1.05 |
| -CºN | 0.23 (0.30) | 0.78 (0.75) | 0.58 (0.53) | -OCOR | 2.09 | - 0.40 | - 0.67 |
| -C=C | 0.98 | - 0.04 | - 0.21 | -Ar (Ph) | 1.35 (1.43) | 0.37 (0.39) | - 0.10 (0.06) |
| -C=C (conj.) | 1.26 | 0.08 | - 0.01 | -Cl | 1.00 (1.05) | 0.19 (0.14) | 0.03 (0.09) |
| -C=O | 1.10 | 1.13 | 0.81 | -Br | (1.02) | (0.33) | (0.53) |
| -C=O (conj.) | 1.06 | 1.01 | 0.95 | -SR | 1.00 | - 0.24 | - 0.04 |
| -NR (R aliph.) | 0.69 | - 1.19 | - 1.31 | -SO2- | 1.58 | 1.15 | 0.95 |
| -NR (R conj.) | 2.30 | - 0.73 | - 0.81 |
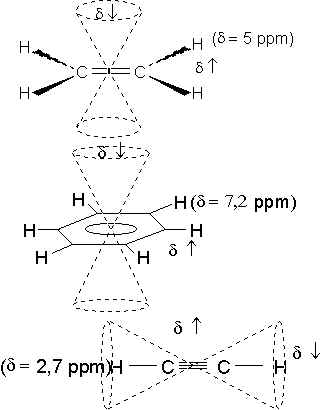
Il est intéressant de déterminer la cause des valeurs élevées des déplacement chimique des protons aromatiques et éthyléniques, alors que celui du proton acétylénique est relativement faible.
Placés dans un champ magnétique, les électrons p du noyau benzénique peuvent être considérés comme deux éléments de courant, s’opposant au champ magnétique appliqué. Ils créent autour du noyau des zones d’anisotropie magnétique provoquant pour les protons situés dans ces zones un déplacement du signal correspondant, soit vers les champs faibles (déblindage), soit vers les champs forts (blindage)
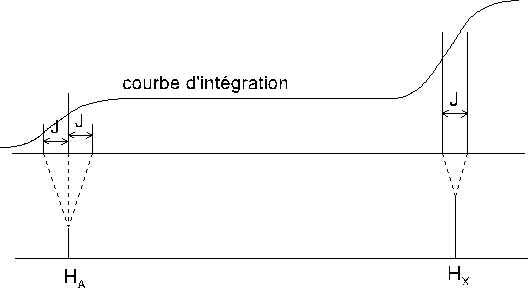
Dans un spectre RMN l’énergie absorbée par une espèce donnée de protons est proportionnelle au nombre de protons mis en jeu. C’est-à-dire que l’intensité du signal, qui est mesurée par sa surface, est proportionnelle au nombre de protons intéressés. Avec les spectrographes courants l’intégration des aires des signaux peut être obtenue directement et se présente sous la forme d’une série de paliers (figure suivante). La hauteur de chaque palier est proportionnelle à l’aire intégrée du signal correspondant.
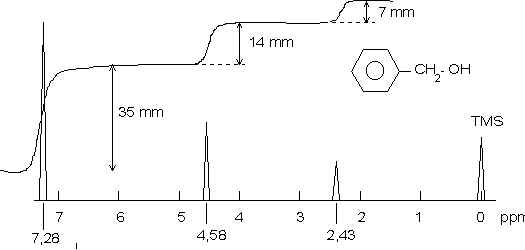
Le spectre représenté ci-dessus est celui de l’alcool benzylique. La hauteur du palier correspondant aux protons aromatiques est de 35 mm. Celle du palier correspondant au groupe –CH2– est de 14 mm, soit bien les 2/5 de 35 mm. Même raisonnement pour le proton de la fonction alcool.
Il est très important de noter que l’intégration ne fournit pas le nombre de protons en valeur absolue. On pourrait tout aussi bien avoir un nombre de protons égal à 10, 4 et 2 pour le spectre ci-dessus.
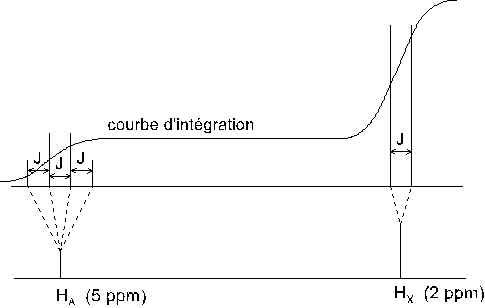
Application à des mélanges
Le spectre suivant correspond à un mélange d’alcool benzylique et de 1,3,5-triméthylbenzène (mésitylène : dAr–H = 6,78 ; dméthyl =2,25). La courbe d’intégration permet de doser les constituants du mélange :
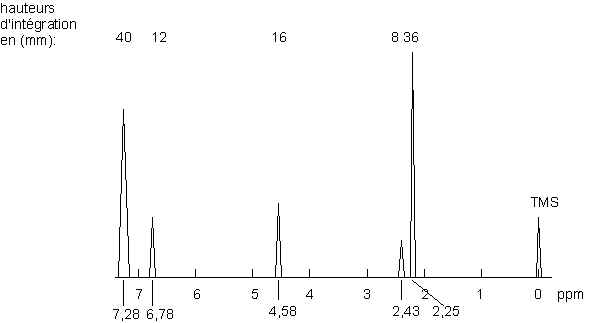
On remarque que 1 proton de l’alcool benzylique intègre pour 8 mm (d = 2,43 ppm), et que 3 protons du mésitylène intègrent pour 12 mm (d = 6,78 ppm). On ramène tout à 1 (de manière à rapporter à 1 molécule de chaque produit : 1 molécule d’alcool benzylique ¾ ® 8 mm et
1 molécule de mésitylène ¾ ® 4 mm
Il y a donc deux fois plus d’alcool benzylique que de mésitylène dans le mélange : 67% et 33%.
2.5.1. Phénomène de couplage
Dans le spectre d’un composé dissymétrique du type A2CH – HCX2 dans lequel A et X provoquent une différenciation considérable du déplacement chimique des protons H(A) et H(X) , les signaux de ces mêmes protons ne se présentent pas sous la forme de raies uniques, mais sous la forme de deux doublets centrés sur les fréquences auxquelles résonneraient H(A) et H(X) s’ils n’étaient pas couplés. La même distance J mesurée en Hertz sépare les composantes de ces deux doublets et elle est indépendante du champ magnétique appliqué.
On peut donner de ce phénomène la représentation simpliste qui suit : Le proton H(X) peut être considéré comme un petit aimant, qui, lorsqu’il est de spin ± ½ , induit un champ local, DH au niveau du proton H(A) . Ce champ local DH ,évidemment indépendant du champ appliqué H0 , se retranche du champ H0 lorsque H(X) est de spin – ½ . Le proton H(A) est donc soumis, suivant le spin de H(X) , aux champs H0 – DH ou H0 + DH et il va résonner à l’une des deux fréquences suivantes :
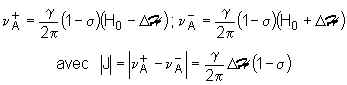
Le champ DH étant indépendant de H0 , J est indépendant de H0 et on le mesure en Hertz. Il est à noter que cette explication n’a pas le moindre sens physique. Elle permet cependant d’arriver à des résultats en accord avec l’expérience.
2.5.2. Spectres de types simples.
Le calcul du spectre théorique de deux protons HA et HB couplés entre eux avec une constante de couplage J conduit aux résultats schématisés ci-dessous :
Le spectre se compose de quatre raies
systématiquement disposées par rapport à la fréquence ![]() et dont les
positions sont données par la relation :
et dont les
positions sont données par la relation :
![]()
(On pose ![]() ) .
L’intensité des composantes extérieures de ce système est proportionnelle à I –
J/D ;
) .
L’intensité des composantes extérieures de ce système est proportionnelle à I –
J/D ;
Comme le montre la figure précédente, l’allure du spectre de deux protons couplés entre eux varie selon le déplacement chimique relatif Dn des deux protons et selon la valeur du couplage J.
Lorsque le déplacement chimique Dn est grand devant J , il est d’usage de désigner les deux protons par deux lettres très espacées dans l’alphabet (A et X par exemple). Lorsque Dn est de l’ordre de grandeur de J ils seront nommés A et B . Deux protons de même déplacement chimique seront nommés A et A .
Cette nomenclature est facilement généralisée à
plusieurs protons. Trois protons conduiront à un spectre ABX si ![]() est du même
ordre de grandeur que JAB , JAX et JBX et si
est du même
ordre de grandeur que JAB , JAX et JBX et si
![]() et
et ![]() >> JAB , JAX et
JBX .
>> JAB , JAX et
JBX .
2.5.2.1. Dn >> J : spectre de type AX.
Le spectre se compose de quatre raies d’égale intensité se répartissant en deux doublets symétriques par rapport aux fréquences nA et nB .
2.5.2.2. Spectres de type AX2.
Considérons un proton HA couplé avec
deux protons HX magnétiquement équivalents et tels que la constante
de couplage JAX de HA avec chaque HX soit la
même et que JAX soit très petit devant ![]() . Le spectre
présente l’allure suivante : Le proton HA donne naissance à un
triplet dont les composantes (d’intensité relative 1-2-1) sont séparées par un
intervalle J, les protons HX donnent naissance à un doublet dont les
composantes d’intensité égale sont séparées par le même intervalle J
.
. Le spectre
présente l’allure suivante : Le proton HA donne naissance à un
triplet dont les composantes (d’intensité relative 1-2-1) sont séparées par un
intervalle J, les protons HX donnent naissance à un doublet dont les
composantes d’intensité égale sont séparées par le même intervalle J
.
2.5.2.3. Spectres de type AX3.
On peut de la même manière reconstituer le spectre d’un composé tel que CH3 – CHBr2 , qui présente des déplacements chimiques valant environ 2 ppm pour les trois protons du méthyle et 5 ppm pour le proton de CHBr2 :
D’une manière générale, on montre que le spectre
d’un proton HA couplé avec n protons équivalents est un multiplet
composé de n + 1 raies dont les intensités relatives sont comme les nombres du
triangle de Pascal (ou comme les coefficients du binôme ![]() .
.
2.5.2.5. Autres types de spectres.
Nous étudierons ces spectres au cas par cas (type ABX , ABC , AB2 , etc ...)
2.5.3. Valeurs des constantes de couplage (en Hz).
|
|
0 | 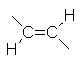 |
11 à 18 | 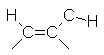 |
0 à 1,5 | 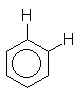 |
6 à 9 |
|
|
2 à 9 |
|
6 à 14 |
|
0,5 à 2 |
|
1 à 3 |
|
|
10 à 13 |
|
0,5 à 3,5 |
|
4 à 10 |
|
0 à 1 |
|
|
1 à 3 |
|
6,7 à 7,2 |
|
5,7 à 6,8 |