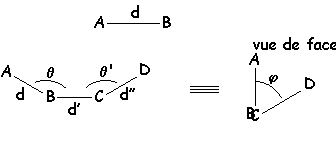
1. Facteurs définissant la géométrie des molécules.
Il faut connaître les distances interatomiques et l’angle θ des diverses liaisons que fait un atome. Pour plus de 4 atomes successifs, il faut également connaître l’angle de torsion j
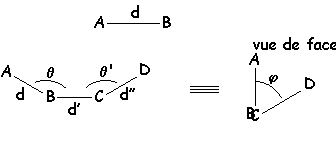
Dans les molécules hydrocarbonées c’est l’angle de torsion (ou angle dièdre) entre les liaisons C ––– C qui importe.
Le butane est ainsi représenté dans l’espace :

Les modifications de la géométrie résultant de la variation de cet angle φ par rotation autour de l’axe C–––C changent la conformation de la molécule.
La configuration d’une molécule de constitution définie est la disposition de ces atomes dans l’espace, sans tenir compte de celles qui ne se différencient que par rotation autour d’une liaison, par exemple :
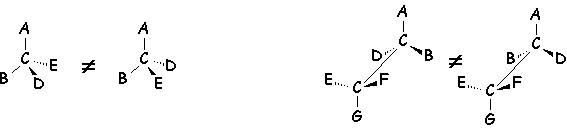
En général, il suffit de 15 kJ.mol–1 pour passer d’une conformation à une autre. On ne pourra donc pas isoler les conformères les uns des autres, alors que les isomères de configuration sont facilement séparables.
Elles sont accessibles grâce à la diffraction électronique et à la diffraction des rayons X . Leur connaissance permet d’attribuer à chaque atome un rayon de covalence : = longueur de liaison. Voici quelques valeurs (en nm) :
| H entre 0,028 et 0,037 | C : 0,0772 | N : 0,074 | O : 0,074 | F : 0,072 |
| B : 0,081 | Si : 0,117 | P : 0,110 | S : 0,104 | Cl : 0,099 |
| Ge : 0,122 | As : 0,121 | Se : 0,117 | Br : 0,114 | |
| Sn : 0,140 | Sb : 0,141 | Te : 0,137 | I : 0,133 |
Pour les atomes doublement et triplement liés, il y a diminution du rayon de covalence :
| C¾ : 0,0772 | N¾ : 0,074 | O¾ : 0,074 |
| C= 0,0667 | N= 0,062 | O= 0,062 |
| Cº 0,0603 | Nº 0,055 | Oº 0,055 |
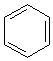 Lorsqu’il y a
résonance, on constate une nouvelle contraction de la liaison. Dans le benzène de
Kékulé , on peut imaginer qu’en moyenne le rayon de covalence est égal à (0,0772
+ 0,0667)/2 = 0,0720 nm. On trouve en réalité 0,070 nm.
Lorsqu’il y a
résonance, on constate une nouvelle contraction de la liaison. Dans le benzène de
Kékulé , on peut imaginer qu’en moyenne le rayon de covalence est égal à (0,0772
+ 0,0667)/2 = 0,0720 nm. On trouve en réalité 0,070 nm.
Les liaisons simples C–––C varient selon le type de carbone :
| tétraédrique | trigonal | linéaire | |
| tétraédrique | 0,154 | 0,150 | 0,146 |
| trigonal | 0,148 | 0,143 | |
| linéaire | 0,138 |
Pour un carbone trigonal α = 120° . En réalité, les angles ne sont pas tout à fait ceux que l’on acceptera dans la pratique (109°28’pour un carbone tétraédrique , 120° pour un carbone trigonal), par exemple :
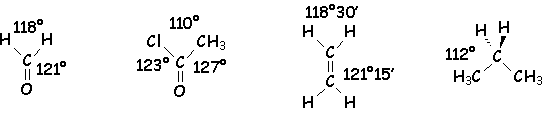
Pour les dérivés azotés : NF3 : 102° ; NH3 :
106°45’;
![]() : 109°
: 109°
1.3.1. Conformations de l’éthane.
La valeur de l’énergie potentielle de la molécule varie en fonction de l’angle dièdre φ entre deux liaisons C ¾ H prises comme référence. Elle est de l’ordre de 12 kJ lorsque les atomes sont en vis-à-vis.
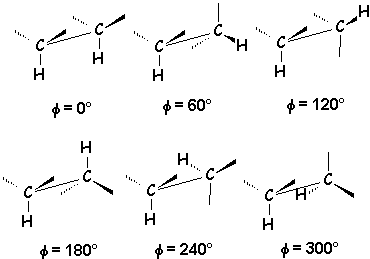
La variation de l’énergie potentielle en fonction de φ est :

On montre qu’il y a 5 molécules sur 1000 en conformation
éclipsée (vis-à-vis). (on a les mêmes conformations pour φ = 0°, 120°, 240° et
φ
= 60°, 180°, 300°, ces trois dernières étant des conformations décalées). Ceci
grâce à la relation de BOLTZMANN :
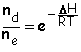 .
.
1.3.2. Conformation du butane.
Il y a quatre conformations remarquables :
La variation d’énergie de formation est maintenant la suivante :

En général, la barrière de rotation augmente quand le volume des substituants s’accroît :
CH3CH2F : 13,8 kJ.mol-1 ; CH3CH2Cl : 14,88 kJ.mol-1 ; CH3CH2Br : 14,92 kJ.mol-1
1.3.3.1. Rotation autour d’une liaison Ctrigonal - Ctétraédrique.
La barrière de rotation s’abaisse :
CH3CH3 : 11,5 kJ.mol-1 ; CH3CH=CH2 : 8,28 kJ.mol-1 ; CH3CH=O : 4,81 kJ.mol-1
Elle s’abaisse encore plus quand le C trigonal porte un autre substituant que H : CH3¾ CO¾ OH : 2 kJ.mol-1 .
1.3.3.2. Rotation autour d’une liaison Ctrigonal — Z
Alors que la barrière de rotation est normale pour une liaison Ctétraédrique — Z , elle est très importante dans le cas présent, à cause de la résonance entre Z et le système π voisin :
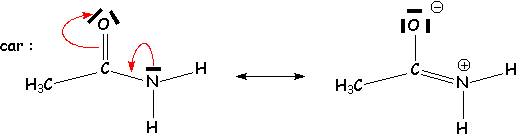
CH3¾ NH2 : 8,11 kJ.mol-1 CH3¾ CO¾ NH2 : 83,6 kJ.mol-1
1.3.3.3. Rotation autour d’une liaison Ctrigonal — Ctrigonal
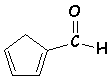 Dans le butadiène nous avons vu que la forme s-trans était plus stable que
la forme s-cis ; la barrière de rotation vaut alors : 21 kJ.mol-1 . Elle est encore plus forte dans le cas
des dérivés carbonylés (C=O) conjugués. Exemple du furfural : la barrière
vaut 42 kJ.mol-1 . (s-trans , le plus stable)
Dans le butadiène nous avons vu que la forme s-trans était plus stable que
la forme s-cis ; la barrière de rotation vaut alors : 21 kJ.mol-1 . Elle est encore plus forte dans le cas
des dérivés carbonylés (C=O) conjugués. Exemple du furfural : la barrière
vaut 42 kJ.mol-1 . (s-trans , le plus stable)
2. Facteurs modifiant la géométrie des molécules
2.1. Moments dipolaires.
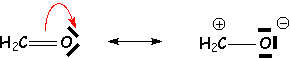 La liaison covalente entre deux
éléments d’électronégativité différente, polarisée par suite du déplacement
électronique vers l’atome le plus électronégatif, fait apparaître des charges
partielles aux extrémités de la liaison:
La liaison covalente entre deux
éléments d’électronégativité différente, polarisée par suite du déplacement
électronique vers l’atome le plus électronégatif, fait apparaître des charges
partielles aux extrémités de la liaison:
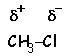 . Cet effet est encore plus marqué dans le cas liaisons multiples
: L’existence de ces dipôles permet d’expliquer la plupart des réactions en
chimie organique. Les moments dipolaires des principales liaisons ont les valeurs
suivantes en DEBYE ( 1 D =
. Cet effet est encore plus marqué dans le cas liaisons multiples
: L’existence de ces dipôles permet d’expliquer la plupart des réactions en
chimie organique. Les moments dipolaires des principales liaisons ont les valeurs
suivantes en DEBYE ( 1 D =
![]() C.m).
C.m).
| H—C | H—Cl | H—Br | H—O | H—S | H—N | H—C | C—Cl | C—Br | C—O | C—N |
| 0,3 | 1,03 | 0,78 | 1,53 | 0,68 | 1,31 | 0,30 | 1,56 | 1,48 | 0,86 | 0,40 |
| C=O | C=S | C=N | CºN | N¾O | N=O | |
| 2,4 | 2,8 | 0,9 | 3,6 | 0,3 | 3,2 | 2,0 |
Calcul du pourcentage ionique d’une liaison : O¾H . On calcule le rapport entre le moment
dipolaire réel et le moment dipolaire théorique obtenu si cette liaison était
totalement ionisée : ![]() :
:
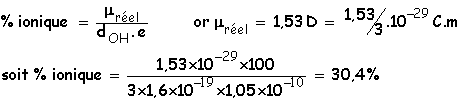
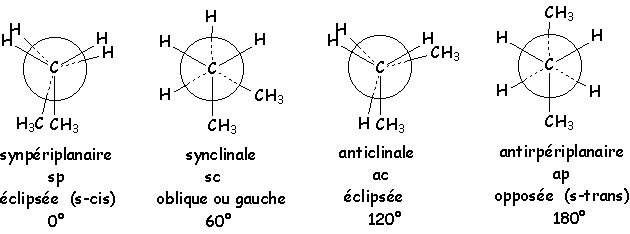
La formation d’une liaison H est susceptible d’intervenir dans les conformations d’une molécule en favorisant l’une d’entre elles, qui peut parfois être la forme éclipsée :

Dans le cas des composés présentant une double liaison, la barrière de rotation est très élevée autour de cette double liaison et le passage d’une forme à l’autre implique la rupture de la liaison π . C’est l’isomérie Z – E.
La définition de cette isomérie dépend d'un classement opéré sur les deux substituants de chacun des deux carbones entourant la double liaison. Ce classement est obtenu par application de règles établies par CAHN , INGOLD et PRELOG :
Le classement (1 et 2) est fondé sur le numéro atomique de chaque substituant. Si pour chacun des deux carbones les vecteurs 1 -> 2 ont le même sens, l'alcène est Z. S'ils sont de sens contraire, l'alcène est E.
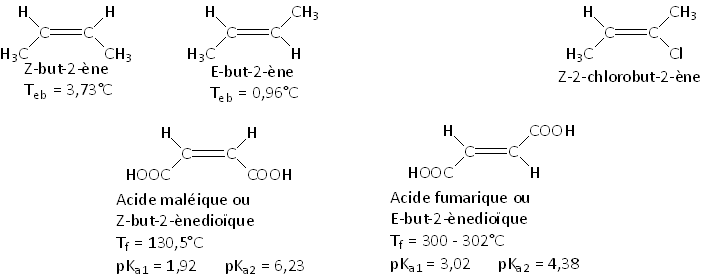
Exemple des but-2-ènes, du 2-chlorobut-2-ène et des acides but-2-ènoïques :
Comme nous le constaterons plus
loin, les diastéréoisomères présentent des propriétés physiques et chimiques
différentes.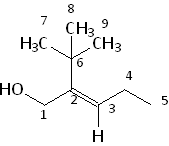
Lorsque les deux atomes fixés sur un des carbones encadrant la double liaison sont identiques, il faut étendre la comparaison aux trois atomes suivants, en respectant les mêmes règles. Prenons l'exemple du 2-tertiobutylpent-2-èn-1-ol :
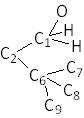
Ici, Il faut commencer par comparer les substituants de premier rang de C1 et de C6 . Ce sont O et C7 . O prime sur C7 ce qui entraîne la primauté de C1 sur C6 . Le 2-tertiobutylpent-2-èn-1-ol représenté ci-dessus est donc E. Si les deux substituants de premier rang sont identiques, il faut reporter la comparaison au second rang, puis au troisième, et enfin, s'il y toujours identité, développer les atomes suivants et recommencer la comparaison.
Lorsqu’on doit comparer un atome doublement ou triplement lié, C=X par exemple, on redouble le substituant en question [X], sur lequel on considère que [C] lui-même est fixé : C - [X] - [C]. [X] sera inférieur à X , mais supérieur à un élément de numéro atomique inférieur. Exemple du 3–éthyl–penta–1,3–diène :
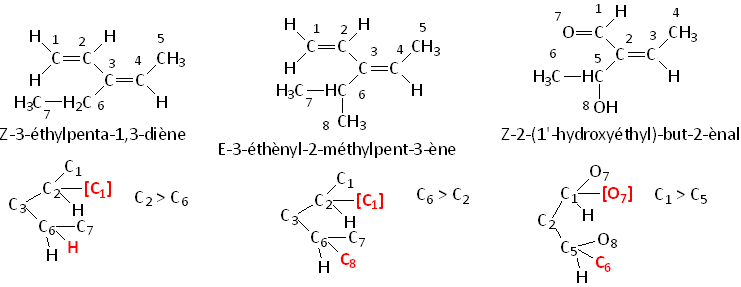
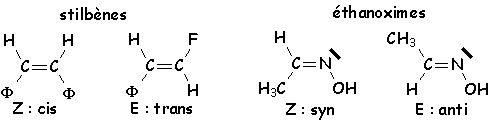 En général, les isomères E sont plus stables, à cause de
l’encombrement stérique entre les gros substituants qui apparaît dans les isomères
Z. Le E–stilbène est plus stable que le Z–stilbène. Une isomérie du
même type se rencontre dans le cas des doubles liaisons C=N . Mais l’isomérisation
procède ici par inversion du doublet de l’azote, à partir d'une température
plus basse que celle permettant la
rotation autour de la double liaison C=C :
En général, les isomères E sont plus stables, à cause de
l’encombrement stérique entre les gros substituants qui apparaît dans les isomères
Z. Le E–stilbène est plus stable que le Z–stilbène. Une isomérie du
même type se rencontre dans le cas des doubles liaisons C=N . Mais l’isomérisation
procède ici par inversion du doublet de l’azote, à partir d'une température
plus basse que celle permettant la
rotation autour de la double liaison C=C :
4.1. Cyclohexane.
Les six atomes du cyclohexane ne peuvent être coplanaires. Il peut présenter plusieurs conformations remarquables :
La conformation chaise à gauche : la plus stable, où tous les atomes sont en position alternée, puis la conformation bateau (à droite).
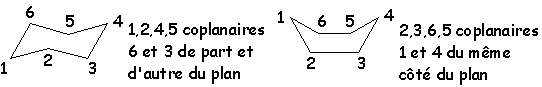
L’énergie de la forme bateau est de 25 kJ.mol–1 plus élevée que celle de la configuration chaise.
Il existe une conformation intermédiaire :
![]()
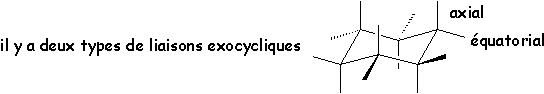
4.1.2. Équilibre conformationnel axial-équatorial
Il est possible de passer d’une conformation chaise à une autre conformation chaise, en changeant les signes de tous les angles. Les positions axiales deviennent équatoriales et réciproquement.
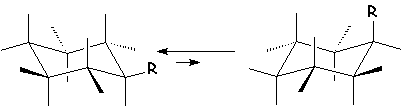
Les substituants les plus encombrants se mettent de préférence en équatorial pour éviter l’interaction qu’ils subissent en axial avec les H axiaux. Ainsi le tertiobutylcyclohexane a deux conformations chaises :
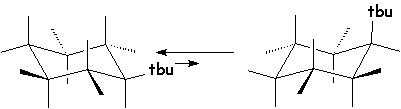
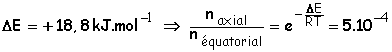 (relation
de Boltzmann).
Donc pratiquement toutes les
molécules possèdent la première conformation, où le groupement tertiobutyl est
en équatorial.
(relation
de Boltzmann).
Donc pratiquement toutes les
molécules possèdent la première conformation, où le groupement tertiobutyl est
en équatorial.
Autre exemple : le 1,3–diméthyl–cyclohexane cis.
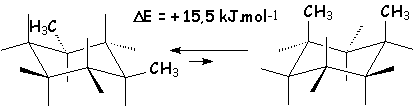
Voici quelques valeurs de DE en fonction du type de substituant :
| Substituant | –F | –CN | –Cl | –OH | –OCH3 | –NH2 | –CO2Me | –CH3 | –C6H5 |
|
|
0,63 | 0,71 | 1,80 | 3,30 | 2,51 | 5,80 | 5,31 | 7,11 | 12,50 |
exemple : calcul du pourcentage de chaque conformère du 1–chloro–3–méthoxy–cyclohexane trans :
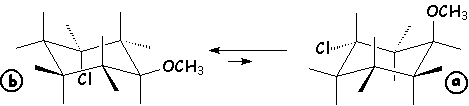
Lorsque les deux substituants sont en axial pour l'un , et en équatorial pour l'autre, l'enthalpie de la réaction ci-dessus est obtenue en soustrayant DE(axial) du DE(équatorial) dans la structure de départ : Ici, D'E = 2,51 - 1,8 = 0,71 kJ/mol. L'application de la relation de Boltzmann donne :
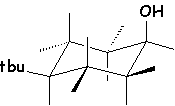
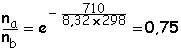 . Donc nb = 57,1
% et na = 42,9 % . À –
250°C ,
. Donc nb = 57,1
% et na = 42,9 % . À –
250°C ,
![]() . Donc nb = 97,6 %.
. Donc nb = 97,6 %.
important : un groupe tertiobutyle impose la conformation où il se retrouve en position équatoriale, quelles que soient les positions des autres substituants.
4.2. Conformation des glucides
Les oses, pentahydroxy–2,3,4,5,6 hexanals, existent sous une forme cyclique (appelée pyranose) obtenue par réaction (hémiacétalisation) du groupe OH porté par C5 avec le groupement aldéhyde. Il y a deux "épimères" possibles : les anomères α et β : cas du glucose

β-D-glucopyranose α-D-glucopyranose
Remarquer que le β-D-glucopyranose est le plus stable de tous les composés qui lui sont stéréoisomères - parmi lesquels on trouve l'α-D-glucopyranose - car tous les gros substituants sont en équatorial.
5. Chiralité et configuration des molécules organiques.
La chiralité est la propriété que possède un objet qui n’est pas superposable à son image dans un miroir :
5.1. Configuration de l’atome de carbone asymétrique.
5.1.1. Définitions.
Un atome de carbone portant 4 substituants différents constitue un système chiral auquel correspond deux isomères (Représentation de CRAM).
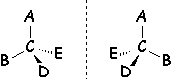
Ces deux isomères sont appelés énantiomères. Les distances interatomiques entre les différents substituants étant les mêmes dans les deux cas, les propriétés physiques et chimiques des deux énantiomères sont les mêmes, à l’exception des propriétés douées d’un caractère chiral.
La mesure du pouvoir rotatoire permet de distinguer les énantiomères. La lumière peut en effet être polarisée :
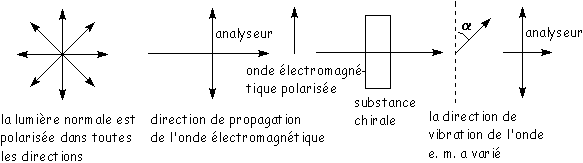
Le dernier analyseur (a) ne laisse passer la lumière que si on le fait tourner d’un angle a par rapport au premier.
Les énantiomères qui dévient vers la droite le plan de polarisation sont appelés dextrogyres, s’ils le dévient vers la gauche, il s’agit de lévogyres. Deux énantiomères ont des pouvoirs rotatoires opposés. Les réactifs chimiques chiraux et les réactifs biologiques (enzymes chiraux) permettent de séparer les énantiomères.
Le mélange en parties égales des deux énantiomères est appelé racémique. La séparation des deux énantiomères est appelée dédoublement ou résolution. Généralement les points de fusion des deux antipodes optiques (énantiomères) sont identiques, alors que celui du racémique est différent.
A partir de matières premières achirales, on obtient le racémique lors d’une synthèse. Par contre les synthèses enzymatiques donnent des produits optiquement actifs purs.
5.1.2. Représentation conventionnelle du C asymétrique.
5.1.2.1. Convention de FISCHER
Les atomes ou groupes d’atomes fixés sur un centre tétraédrique sont projetés sur le plan du papier de telle façon que les atomes ou groupes d’atomes apparaissant au dessus ou au dessous se trouvent en arrière du plan du papier et ceux qui apparaissent à droite et à gauche de l’atome central se trouvent en avant du plan du papier. La chaîne principale est dessinée verticalement avec le chaînon de plus petit indice en haut.
Dans les représentations spatiales, ![]() représente une liaison qui se dirige depuis le plan du papier vers
l’observateur,
représente une liaison qui se dirige depuis le plan du papier vers
l’observateur, ![]() représente une liaison
s’éloignant de l’observateur.
représente une liaison
s’éloignant de l’observateur.
Exemple des aldéhydes glycériques ou 2,3-dihydroxy-propanal :
![]()
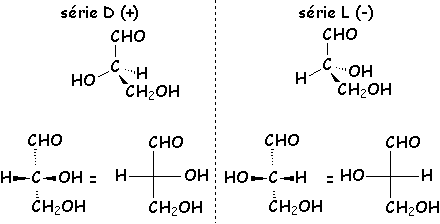
Dans la représentation de Fischer des oses, un énantiomère est D si le carbone d'indice nmax - 1 porte OH à droite. Il est L si cet OH est à gauche.
L’appartenance à la série D ou L n’implique pas que les composés soient dextrogyres ou lévogyres ; le sens du pouvoir rotatoire est indiqué par (+) ou (-). Cependant Fischer a défini la convention D / L à partir du pouvoir rotatoire (+) / (-) de l'aldéhyde glycérique.
5.1.2.2. Règle séquentielle de CAHN, INGOLD et PRELOG.
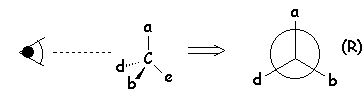 Les quatre
substituants sont placés suivant un ordre de priorité, d’après les règles
précises déjà vues : a > b > d > e . Si un observateur, regardant dans la
direction C––e est placé à l’opposé de e par rapport à l’atome de
C , voit la séquence a → b
→ d en tournant dans le sens des aiguilles
d’une montre, l’atome de carbone est désigné par le symbole R (rectus). Dans
le cas contraire par S (sinister).
Les quatre
substituants sont placés suivant un ordre de priorité, d’après les règles
précises déjà vues : a > b > d > e . Si un observateur, regardant dans la
direction C––e est placé à l’opposé de e par rapport à l’atome de
C , voit la séquence a → b
→ d en tournant dans le sens des aiguilles
d’une montre, l’atome de carbone est désigné par le symbole R (rectus). Dans
le cas contraire par S (sinister).
Rappel des règles de préséances :
– les atomes sont rangés dans l’ordre des numéros atomiques décroissants :
acide bromochloroéthanoïque
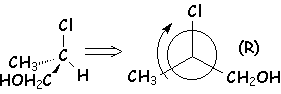 – lorsque deux
atomes identiques sont fixés sur le carbone asymétrique, c’est celui qui porte un
substituant de rang plus élevé qui l’emporte : 2-chloro-propan-1-ol
– lorsque deux
atomes identiques sont fixés sur le carbone asymétrique, c’est celui qui porte un
substituant de rang plus élevé qui l’emporte : 2-chloro-propan-1-ol
– lorsqu’un atome est doublement lié, son rang devient comparable à celui d’un atome lié à deux groupes équivalents. On fait figurer le deuxième atome entre crochets, car l’existence d’un autre carbone portant effectivement ces deux atomes fait passer celui-ci devant celui-là :
3,4 -diméthyl-pent-1-ène
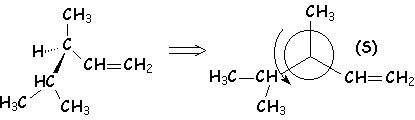
– par contre, si on a un atome de rang plus bas à comparer avec celui entre crochets, c’est celui-ci qui l’emporte : L-glycéraldéhyde
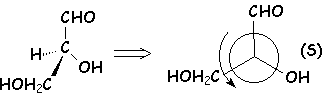
La détermination de la configuration absolue n’a été résolue qu’en 1951 grâce à la diffraction des rayons X. Par hasard, la configuration absolue de l’aldéhyde glycérique s’est révélée conforme à celle admise par FISCHER. L’emploi des méthodes optiques est de loin préférable à l’étude des filiations chimiques pour parvenir à la configuration absolue.
En représentation de FISCHER, un aminoacide D
![]() est représenté ainsi : Si R est un
cycle benzénique, il s'agit alors de la D-phénylanaline.
est représenté ainsi : Si R est un
cycle benzénique, il s'agit alors de la D-phénylanaline.
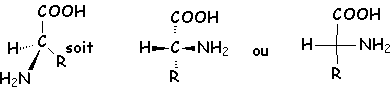
Il est donc R.
Les acides aminés naturels sont la plupart du temps L
5.1.5 Diverses méthodes pratiques permettant de déterminer la configuration absolue d'un carbone asymétrique.
La détermination de la configuration R,S peut se faire à partir de la représentation de FISCHER, en tournant du plus gros au troisième en taille lorsque le plus petit substituant est sur la verticale, et du troisième au premier lorsque le plus petit substituant est sur l’horizontale.
De même, lorsque dans une représentation de
CRAM le plus petit substituant pointe vers l'observateur, il est pratique de
décrire les autres substituants dans le sens 3 → 2 → 1, ce qui
permet d'obtenir facilement la configuration absolue.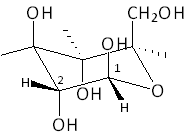
Exemple : Quelle est la configuration absolue du carbone 1 du b-D-glucopyranose ?
L'ordre de préséance des substituants est : O - C ; O - H ; C2. Comme H, le plus petit substituant, pointe vers l'observateur, la configuration absolue est obtenue en décrivant les substituants dans le sens C2 → O - H → O - C, soit le sens des aiguilles d'une montre. C1 est donc R.
5.1.6 Dédoublement des énantiomères.
Le dédoublement (ou résolution) des énantiomères à partir d'un mélange racémique par exemple, est réalisé en faisant réagir le composé avec un autre composé chiral énantiomériquement pur. On obtient alors deux diastéroisomères que leurs propriétés chimiques différentes permettent de séparer ( cristallisation fractionnée, chromatographie sur colonne,...).
Exemple :
Le dédoublement des deux énantiomères de la 1-phényléthanamine peut être obtenu par cristallisation différentielle des sels obtenus par réaction acide-base avec l'acide tartrique like (RR) :
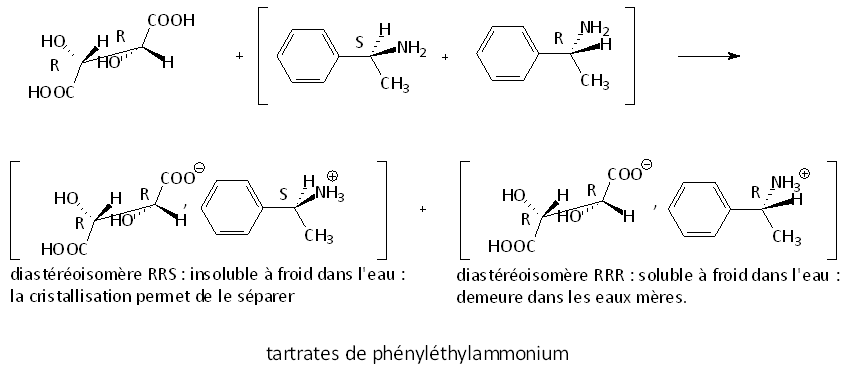
Dans les deux cas, le traitement par la soude permet de récupérer l'amine (insoluble dans l'eau). Le diastéréoisomère RRS libère l'amine S, le RRR libère l'amine R.
5.2. Chiralité due aux hétéroatomes
5.2.1. Atomes quadriliés
 Sn et Si jouent le même rôle que C.
Sn et Si jouent le même rôle que C.
Les sels d’ammonium et de phosphonium peuvent également être chiraux :
Avec les sels de sulfonium, il apparaît un dédoublement :
Par contre dans le cas des amines, qui devraient être
dédoublables, on a une structure pyramidale qui s’inverse très rapidement aux températures ordinaires :
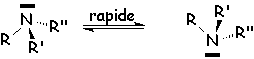
Le temps d’inversion de ![]() est de 2,5.10-11 s. Il en est de même
pour les carbanions
est de 2,5.10-11 s. Il en est de même
pour les carbanions ![]() . Par contre, toujours à
298°K,
. Par contre, toujours à
298°K, ![]() s’inverse en 2,3.10-6 s, et
s’inverse en 2,3.10-6 s, et
![]() en 1,4 année. La racémisation est très lente dans
ce dernier cas et on peut séparer les énantiomères.
en 1,4 année. La racémisation est très lente dans
ce dernier cas et on peut séparer les énantiomères.
5.3. Chiralité en l'absence de carbone asymétrique.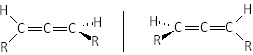
Le phénomène de chiralité s'observe dans certaines structures particulières, par exemple dans les composés allèniques, où les plans formés par les substituants et les carbones qui les portent sont perpendiculaires : Les deux structures ci-contre sont l'image l'une de l'autre par rapport au plan vertical tracé, mais ne sont pas superposables : ce sont donc des énantiomères
Lorsqu’une molécule présente deux centres asymétriques, il existe deux couples d’énantiomères, dits diastéréoisomères, qui ne sont pas images l’un de l’autre
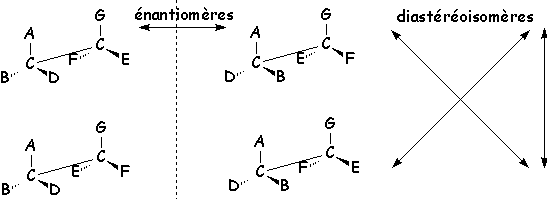
Les propriétés physiques des diastéréoisomères sont différentes, ils sont donc séparables par les méthodes usuelles (fusion fractionnée, distillation,...).
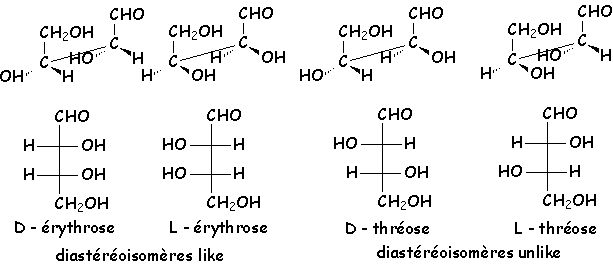
5.4.1. Isomérie like - unlike (précédemment érythro - thréo)
Cette isomérie est un cas particulier de diastéréoisomèrie,
valable uniquement lorsque, dans une molécule comportant deux carbones asymétriques,
chacun de ces deux carbone porte au moins deux substituants identiques deux à deux.
Prenons l’exemple de l’érythrose et du thréose (sucres aldéhydiques en C4), d’où vient d’ailleurs le
nom de cette isomérie :
![]() Lorsque les
configurations absolues des deux carbones asymétriques sont identiques (RR ou
SS), on parlera de diastéréoisomère like. Inversement, si les
configurations absolues sont opposées (RS ou SR), on parlera de diastéréoisomère
unlike.
Lorsque les
configurations absolues des deux carbones asymétriques sont identiques (RR ou
SS), on parlera de diastéréoisomère like. Inversement, si les
configurations absolues sont opposées (RS ou SR), on parlera de diastéréoisomère
unlike.
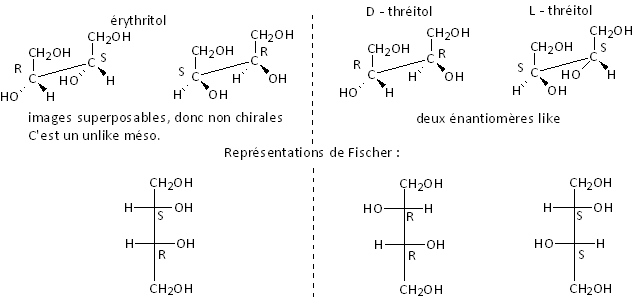
Autre exemple : l’érythritol et le thréitol, les
butane-1,2,3,4-tétrols :
![]() . Dans ce cas, il n'existe qu'un
seul diastéréoisomère unlike, non dédoublable, que l'on appelle méso.
Les diastéréoisomères RR et SS, qui sont énantiomères entre eux, sont des
like.
. Dans ce cas, il n'existe qu'un
seul diastéréoisomère unlike, non dédoublable, que l'on appelle méso.
Les diastéréoisomères RR et SS, qui sont énantiomères entre eux, sont des
like.
5.4.2. Cas de plusieurs carbones asymétriques
5.4.2.1. Trois C asymétriques
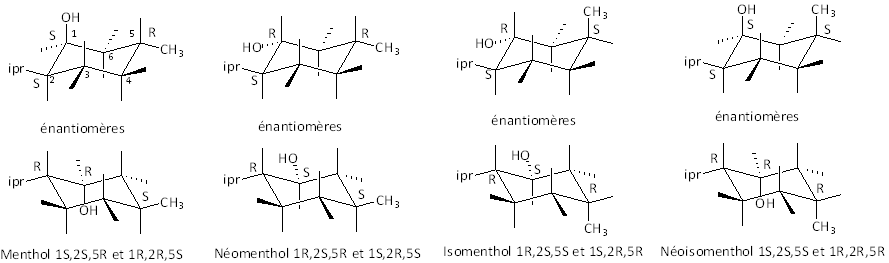
Il y 23 = 8 stéréoisomères formants 4 couples d’énantiomères. Ces couples présentent la relation de diastéréoisomèrie entre eux. Exemple du menthol :
ce sont les conformations les plus stables qui sont indiquées.
"ipr" signifie isopropyl.
À partir des pentoses
![]() ,
on peut obtenir les acides pentariques
,
on peut obtenir les acides pentariques
![]() . Il
n’y a que deux véritables C asymétriques. Le C central est dit pseudoasymétrique.
Les quatre stéréoisomères ne se répartissent pas en like RR et SS, et unlike RS
et SR, mais en
deux énantiomères optiquement actifs et deux mésos sans activité optique :
. Il
n’y a que deux véritables C asymétriques. Le C central est dit pseudoasymétrique.
Les quatre stéréoisomères ne se répartissent pas en like RR et SS, et unlike RS
et SR, mais en
deux énantiomères optiquement actifs et deux mésos sans activité optique :
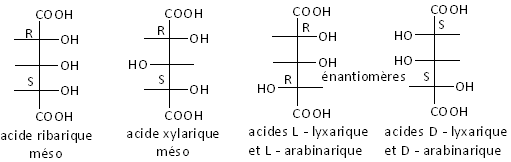
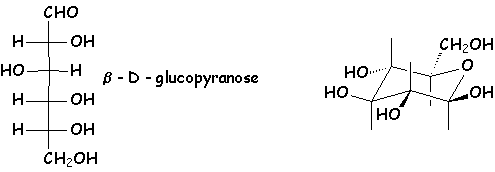 Il y a 24 = 16 isomères, donc 8 couples de
diastéréoisomères, ayant chacun un nom d’usage, tel les D et L-glucose :
Il y a 24 = 16 isomères, donc 8 couples de
diastéréoisomères, ayant chacun un nom d’usage, tel les D et L-glucose :
Dans ce cas
là, les 2 carbones asymétriques situés en tête de pont ne comptent que pour un seul
centre asymétrique, le pont ne pouvant être de part et d’autre du plan moyen du
cycle :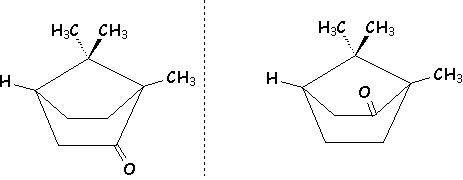
exemple du camphre
Quoiqu’il y ait deux carbones asymétriques, il n’y a que deux énantiomères.