Méthode d'EULER
1) On y va lentement et séparément
définition des fonctions et résolution exacte des équations différentielles
|
> |
restart:with(DEtools):with(plots):f:=(x,y)->(-(x^2)*y-y^2+2*x)/(1-x^3);eq:= D(y)(x)=f(x,y(x)); |
Warning, the name changecoords has been redefined
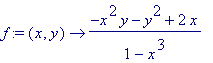
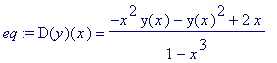
![]()
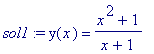
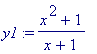
procédure de calcul des
![]() par la méthode d'Euler
par la méthode d'Euler
|
> |
z:=proc(n,xo,yo,f,A) |
initialisations et calcul des
![]() par appel de la procédure
par appel de la procédure
détermination des extrémums des
![]()
|
> |
with(plots): |
![]()
![]()
![]()
![]()
![]()
![]()
tracés simultanés des 4 courbes
|
> |
with(plottools):seq_opt:=x=-0.05..xo,y=min(a1,b1,c1,a2,b2,c2)..max(a1,b1,c1,a2,b2,c2)+0.05,color=black: |
Warning, the names arrow and translate have been redefined
![[Maple Plot]](images/EULER215.gif)
2) Le tout en un
|
> |
restart:with(plots):with(DEtools):with(plottools): |
Warning, the name changecoords has been redefined
Warning, the names arrow and translate have been redefined
|
> |
z:=proc(n1,n2,n3,xo,yo,f) |
On essaie
|
> |
|
> |
f:=(x,y)->(-(x^2)*y-y^2+2*x)/(1-x^3);eq:= D(y)(x)=f(x,y(x)); |
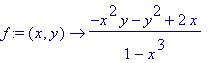
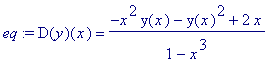
![]()
![[Maple Plot]](images/EULER219.gif)