Page d'accueil Retour vers les ressources de physique Télécharger le document
1 Structure de l’atome
1-1 Structure électronique et nucléaire, particules élémentaires
L’atome est composé d’un noyau autour duquel tournent des électrons.
Le noyau est composé de neutron et de proton, qui sont des nucléons.
|
Atome 6447448 électron noyau 64748 Neutron Proton |
proton p+
neutron n°
électron e-
masse des particules élémentaires
mp ≈ mn ≈ 1830 me
mp ≈ mn ≈ 1,67.10-27 kg
me ≈9,1.10-31 kg
La masse des particules élémentaires au repos est :
mp = 1,6726432.10-27 kg
mn= 1,6748882.10-27 kg
Charge des particules élémentaires
qp = - qe = e = 1,6.10-19 C
1-2 Notation des nucléïdes
On note Z le nombre de proton Z est le nombre de charge
On note A le nombre de nucléon A est le nombre de masse
On note Nle nombre de neutron
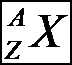 X est le symbole du nucléïde.
X est le symbole du nucléïde.
On notera le proton le neutron et l’électron de la même manière :
![]()
![]() et
et ![]()
Deux atomes ayant :
le même Z mais un A différent sont des isotopes
le même A mais un Z différent sont des isobares
le même N mais un Z différent sont des isotones
Exemple :
isotopes ![]()
isobares ![]()
isotones ![]()
En nucléaire le symbole ne représente qu’un seul atome et non une mole d’atome.
1-3 Principes fondamentaux
1-3-1 Équivalence masse énergie
D’après la relation d’Einstein, à toute masse m0, il correspond une énergie :
E = m0 c2 avec c = 3.108 m.s-1 (1)
Il en résulte qu’une particule au repos possède une énergie, son énergie de masse au repos.
exemple : calcule de la masse du deutérium à partir de la masse du proton et du neutron. La masse d’un noyau de deutérium est : mD = 3,3445172.10-27 kg
Le noyau de deutérium est ![]() ,
il est composé d’un proton et d’un neutron
,
il est composé d’un proton et d’un neutron
mp+mn= 3,3475314.10-27kg > mD = 3,3445172.10-27 kg
Dm = - 0,0030142.10-27 kg
DE = - 2,71278.10-11 J pour un atome
DE = -1,6330935.1013 j pour 2g de deutérium
1-3-2 Conservation de la charge
Dans toute transformation radioactive ou d’une réaction nucléaire, le nombre de charge se conserve.
1-3-3 Conservation du nombre de nucléon
Dans toute transformation nucléaire, il y a conservation du nombre de masse, donc du nombre de nucléon.
1-3-4 Conservation de l’énergie
L’énergie existe sous diverses formes :
· énergie cinétique ( ½ mv2 )
· énergie potentielle (EK, EL...)
· énergie rayonnante (hn)
Si on considère un système de particules en interaction ce principe s’applique à l’ensemble du système, chaque particules possédant une énergie de masse au repos plus son énergie cinétique.
E = m0c2 + Ec = mc2 (2)
m est la masse relativiste avec :
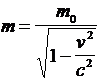 (3)
(3)
Þ m0 c 2 = m c2- m v2
1-3-5 Conservation de l’impulsion
Une particule en mouvement a une impulsion ou quantité de mouvement :
![]()
Au cours de l’interaction, l’impulsion totale du système est conservée. On en déduit la relation entre énergie et impulsion :
E2 = p2c2 + (m0c2)2 (4)
démonstration de la formule (4):
(2) Þ E = m0c2 + Ec = mc2
(3) Þ 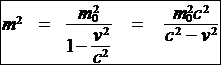
c2 * ê m02c2 = m2c2 - m2v2
m2c4 = m02c4 + p2c2
E2 = m02c4 + p2c2
1-3-6 Dualité onde-corpuscule
En 1905 Einstein montre que l’aspect ondulatoire de la lumière n’est pas la seule manifestation d’une onde électromagnétique. Il émet l’hypothèse qu’à toute onde électromagnétique de fréquence n, peut être associée une corpuscule : le photon dont l’énergie quantifiée est
En = hn = hc/l
où h est la constante de planck h = 6,62.10-34 J.s et c = 3.108 m/s
Pour le photon la masse est nulle, car il se déplace à la vitesse limite de la lumière, donc :
m0c2 = 0
E = pc
p = E/c = hn/c
Il en résulte que les quanta de lumière ont une impulsion p dans la direction de la lumière.
Par analogie Louis de BROGLIE en 1924 émet l’hypothèse réciproque qu’à toute particule d’impulsion p est associée une onde de longueur d’onde
l = c/n = h/p = h/mv
1-4 Grandeurs liées à l’atome
1-4-1 Longueur
le diamètre d’un atome est de l’ordre de grandeur de l’angströme (Å) ( 10-10 m)
Le Rayon de Bohr de l’atome d’hydrogène est rH = 0,59 Å
Le rayon du proton est de l’ordre du femtomètre ( 10-15 m)
Le rayon d’un noyau lourd est de environ 7 fm
Le rayon du noyau de l’atome varie en fonction du nombre de nucléon A :
R = R0. A 1/3 avec R0 = 1,2 fm
1-4-2 Le temps
L’échelles de temps des phénomènes nucléaires est très étendu. Elle varie de 10-20s réaction nucléaire à 109 ans (désintégration nucléaire )
Dans la pratique on utilise l’unité la mieux adaptée au phénomène.
1-4-3 Énergie
L’unité d’énergie en nucléaire est l’électron-volt (eV).
1 eV = 1,6.10-19 J 1 J = 0,625.10+19 eV = 0,625.10+13 MeV
1-4-4 Masse
L’unité légale de masse est le kg. Beaucoup trop grand pour les atomes :
(mp ≈ mn ≈ 1,67.10-27 kg)
On va donc utiliser des unités mieux adaptées :
· L’unité de masse atomique ( u )
1 u est le 1/12 de la masse d’un atome de carbone 12 ( 12C)
or une mole de carbone 12 a une masse de 12 g
donc :
![]()
· MeV.c-2
à chaque masse m0 peut être associée une énergie : l’énergie de masse
E = m0.c2 avec c= 3.108 m/s E en joules m en kg
si E en MeV
1 MeV = 1,6.10-13 J 1 J = 0,625.1013 MeV
Pour déterminer la masse en MeV.c-2 on calcule l’énergie de la masse m0 en MeV :
exemple : masse du proton au repos mp = 1,67.10-27.kg
E = 1,67.10-27.9.1016 J
![]()
E = mp .c2
mp = 939,375 MeV.c--2
Valeurs des masses des particules élémentaires
|
masse en |
u |
MeV.c--2 |
|
e- |
5,485.10-4 |
0,511 |
|
p+ |
1,00727 |
938,28 |
|
n0 |
1,00866 |
939,57 |
|
u |
1 |
931,5 |
|
a |
4,00150 |
3727,41 |
2 Modèle atomique
2-1 Structure électronique postulat de Bohr
· Un électron, dans un atome, décrit une orbite autour du noyau sous l’influence de l’attraction Coulombienne entre électron et noyau .
· Le moment angulaire orbital de l’électron L = mnr ne peut varier que de manière discrète. Il est quantifié seules sont permises les orbites pour lesquelles :
2pL = nh avec n = 1,2,3,...
· Sur une orbite permise l’électron, bien que constamment accéléré ne rayonne pas d’énergie. Son énergie totale est constante.
· Un rayonnement électromagnétique n’est émis que si un électron saute d’une orbite d’énergie Ei sur une autre orbite permise d’énergie inférieure Ef .
L’énergie rayonnée est
E = Ef - E i < 0 (E<0 car énergie cédée)
Chaque orbite correspond à un état d’énergie de l’atome.
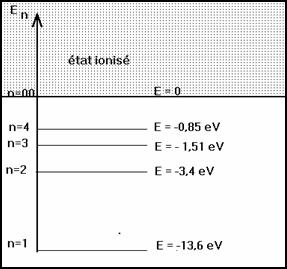
2-2 Niveaux d’énergie
L’énergie totale de l’électron sur un niveau d’énergie est la somme de son énergie potentielle et de son énergie cinétique Ec. l’énergie potentielle est nulle si l’électron est à l’infini.
En = Ep + Ec ![]()
or ![]() ð
ð ![]() donc
donc ![]()
Le moment cinétique 2pL = nh avec
![]()
L = nh = mvr
On montre que pour l’atome d’hydrogène Z = 1
![]()
|
|
Pour n > 1 les états sont excités et instables ; la durée de vie dans un état excité est de l’ordre de la nanoseconde ( 10-9 s).
Pour n = 1 l’atome est dans l’état fondamental.
Pour n = ∞ l’atome est ionisé.
2-3 Nombres quantiques, structure hyperfine
n nombre quantique principal n = 1, 2, 3 ,...
· l nombre quantique azimutal l = 0 ,1 ,2 ,3 ,....
· ml nombre quantique magnétique ml = -l ,-l+1 ,....,0 ,1 ,2 ,...., l-1 ,l
· s spin s = ± ½
n correspond au niveau d’énergie
ml correspond au moment cinétique ( sens de rotation de l’électron autour du noyau. C’est une charge électrique qui tourne donc crée un champ magnétique)
s le spin correspond à la rotation de l’électron sur lui-même.
2-4 Principe d’exclusion de Pauli
Si un atome a un numéro atomique Z la charge autour du noyau est Ze
Les Z électrons ne peuvent pas avoir le même état quantique.
Il faut donc que les 4 nombres quantiques ne soient pas identiques pour 2 électrons quelconques.
2-5 Configuration électronique d’un atome
Pour un même niveau d’énergie le nombre quantique n est le même.
|
niveau |
n |
l |
m |
s |
états |
|
K |
n = 1 |
l = 0 |
m = 0 |
s = ± ½ |
1s2 |
|
L |
n = 2 |
l = 0 l = 1 |
m = 0 m = 0, ± 1 |
s = ± ½ s = ± ½ |
2s2 2p6 |
|
M |
n = 3 |
l = 0 l = 1 l = 2 |
m = 0 m = 0, ± 1 m = 0, ± 1, ± 2 |
s = ± ½ s = ± ½ s = ± ½ |
3s2 3p6 3d10 |
|
N |
n = 4 |
l = 0 l = 1 l = 2 l = 3 |
m = 0 m = 0, ± 1 m = 0, ± 1, ± 2, ± 3 m = 0, ± 1, ± 2, ± 3, ± 4 |
s = ± ½ s = ± ½ s = ± ½ s = ± ½ |
4s2 4p6 4d10 4f14 |
L’énergie de liaison d’un électron varie de quelques électrons-volts à quelques centaines de keV pour les atomes les plus lourds et les électrons les plus liés ( les plus profonds).
A l’état fondamental les électrons d’un atome sont au niveau le plus bas possible.
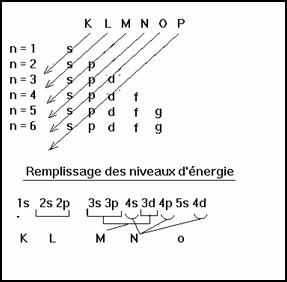
Ordre de remplissage des niveaux d’énergie par les électrons
|
|
Le remplissage du sous niveau 3d correspond à la série des Lanthanides et celui des 4d à la série des actinides.
Les Lanthanides sont tous dans la case 57 du tableau de Mendeleïev et les actinides sont tous dans la case 89 de l’actinium.
Il est à noter qu’il y a quelques irrégularité dans le remplissage au niveau du nickel et cuivre, du Technétium et Ruthénium, ainsi que de l’iridium et platine.
2-6 Le noyau
2-6-1 États d’énergie du noyau.
Le noyau ![]() contient
Z protons et N = A - Z neutrons.
contient
Z protons et N = A - Z neutrons.
L’énergie du noyau au repos est :
M(A,Z) c2 = Z Mp c2 + N Mn c2 - B
avec Mp c2 = 938,28 MeV énergie de masse du proton
Mn c2 = 939,59 MeV énergie de masse du neutron
B énergie de liaison totale des A nucléons, ou défaut de masse ( B ð Binding : liaison en anglais).
On appelle ![]() l’énergie
moyenne de liaison par nucléon.
l’énergie
moyenne de liaison par nucléon.
On peut constater que cette énergie de liaison par
nucléon est maximum de A = 60 à A = 90. Cela correspond aux noyaux les plus
stables ![]() ≈
9 MeV.
≈
9 MeV.
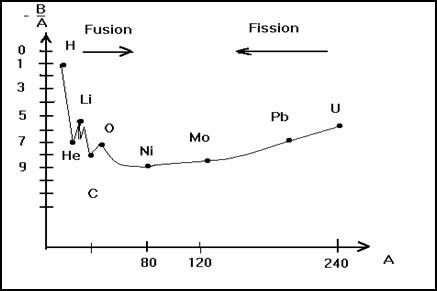
Si A < 30 ![]() varie
peu et est voisine de 8 MeV. C’est une valeur forte comparée à l’énergie de
liaison des électrons. On peut obtenir de 2 façons des noyaux de grande énergie
de liaison par nucléon.
varie
peu et est voisine de 8 MeV. C’est une valeur forte comparée à l’énergie de
liaison des électrons. On peut obtenir de 2 façons des noyaux de grande énergie
de liaison par nucléon.
· Soit en cassant un noyau lourd en deux noyaux plus légers : c’est la fission.
· Soit en assemblant deux noyaux légers en un noyau plus lourd : c’est la fusion
2-6-2 Forces nucléaires
La cohésion du noyau est due à l’interaction nucléaire forte.
Caractéristiques des forces nucléaires :
· Attractives et très intenses (forte énergie de liaison des nucléons)
· De très courte portée ≈ 1 fm (différente de la coulombienne à longue portée en 1/r2 )
· Indépendante de la charge ( les forces d’attraction n-n, p-p et n-p identiques)
· Elles sont saturées. Le vecteur interaction est le méson p
2-6-3 États excités : processus de désexcitation
2-6-3.1 Désexcitation de l’atome
Si le cortège d’électron est modifié par une collision avec un projectile, l’atome se trouve excité dans un état instable de courte durée (10-8 à 10-15 s). Si un proton p+ arrache un électron e- de la couche K, l’atome est ionisé. il y a une vacance électronique.
Il y a désexcitation par un électron de niveau supérieur (en général L) puis M comble L puis N comble M ...
La transition L® K libère une énergie E = EK- EL < 0
La désexcitation peut s’effectuer par deux processus :
· soit une émission X
· soit par effet AUGER
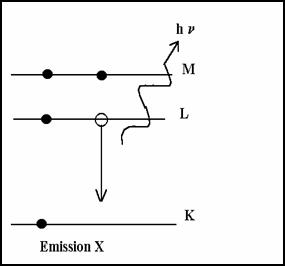
* Emission X
L’énergie est emportée par un photon d’énergie hn
hn = | (EL-EK)| énergie ≈ 120 keV
Il y a un grand nombre d’émission possible, car il y a plusieurs niveaux d’énergie et sous niveaux d’énergie. L’onde électromagnétique est en mode transverse.
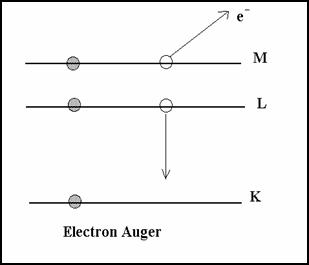
* Effet Auger
Ce processus est non radiatif, l ’énergie disponible est directement transférée sans émission X à un électron du cortège qui est éjecté de l’atome avec une énergie cinétique égale à l’énergie libérée diminuée de l’énergie de liaison de l’électron.
C’est un processus d’auto-ionisation de l’atome. L’effet Auger est prédominant pour les éléments légers. L’émission X prédomine pour les éléments lourds.
Dans l’effet Auger le champ électrique est en mode radial.
Il y a compétition entre émission X et l’effet Auger.
|
|
2-6-3.2 Désexcitation du noyau
Très souvent après émission a ou b ou après une réaction nucléaire (capture, fission, fusion) le noyau est dans un état excité.
Les états d’énergie du noyau sont quantifiés comme ceux de l’atome.
Il existe deux processus de désexcitation du noyau :
· par émission g
· par conversion interne
· Émission g
Ce sont des rayonnements électromagnétiques de même nature que les rayons X mais plus énergétiques, donc de plus grande fréquence.
On montre que l’énergie de recul du noyau est de l’ordre de :
ER = 50 eV
et que l’énergie du photon g est de l’ordre de :
Eg ≈ 2 MeV
donc ER << Eg ≈ Ei -Ef
L’énergie Eg est de l'ordre de 10 keV à 3 MeV.
· Conversion interne
La conversion interne est un processus non radiatif de désexcitation du noyau. L’énergie est cédée directement à un électron du cortège électronique ( le plus souvent du niveau K) qui est éjecté avec une énergie :
Ee- = E - B B énergie de liaison E énergie de désexcitation
A la suite de la conversion interne le cortège électronique se réarrange avec émission de rayon X ou d’électron Auger.
3 La Radioactivité
3-1 Définition
Certains nucléides se transforment spontanément au cours du temps. Cette transformation correspond à un changement de nature du noyau. Cette transformation se fait par émission de particule a ou b ou par fission spontanée ou par capture électronique. Cela se passe pour les noyaux lourds ou qui ont un excès de neutron ou de proton.
Ces noyaux sont dits « Radioactifs » ils se désintègrent. Ce phénomène est indépendant des conditions physico-chimiques du nucléide et de l’âge du nucléide.
La probabilité que, pendant un temps dt, le nucléide considéré se désintègre est une donnée caractéristique de ce nucléide.
3-1-1 Loi de désintégration radioactive
Soit un nombre N(t) d’atomes radioactifs d’une espèce présents à la date t.
Entre t et t + dt un certain nombre de noyaux se sont désintégrés et ont changé de nature.
On appelle dN la variation du nombre d’atome entre ces deux dates. Cette variation est proportionnelle au nombre N(t) d’atomes à la date t, dépend du nucléïde considéré et de la durée dt.
dN = - N l dt (- car il y a diminution de N)
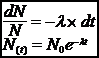
l est la constante radioactive du nucléïde
N0 est le nombre d’atomes présents à la date t = 0
La décroissance radioactive suit une loi exponentielle.
3-1-2 Période radioactive
La période T est le temps nécessaire pour que la moitié des N0 atomes présents à la date t=0 se soient désintégrés.
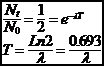
Les périodes T des différents radioéléments couvrent un domaine très vaste, depuis
T > 1030 ans pour le vanadium à
T < 2.96.10-7
s pour ![]()
3-1-3 Vie moyenne
La vie moyenne d’un atome particulier est comprise entre 0 et ∞ . Si on a N0 atomes présents à t = 0 à t il en reste :
N(t) = N0 e -lt
entre t et t + dt , dNt atomes se désintègrent
dN(t) = - l N(t) dt
ces dN(t) atomes ont eu une vie égale à t
La durée de vie totale de l’ensemble est
dN(t) .t = - l N(t) t dt
Par définition la vie moyenne t des N0 atomes est la somme des durées de vie de tous les atomes divisée par N0 .
![]()
or N(t) = N0 e -lt
![]()
on intègre par partie, on obtient t = l-1
or N(t) = N0 e -lt si t = t = l-1
donc N(t) = N0 e -l/l = N0 e-1
![]()
La vie moyenne correspond au temps au bout duquel le nombre d’atomes a décru d’un facteur 1/e.
3-2 Mode de transformation spontanée
On peut classer en deux catégories les modes de transformation :
· Transformation isobarique ( A = cte)
· Transformation par partition en 2 noyaux.
3-2-1 Transformation isobarique
Ce sont des transformations sans changement du nombre de masse A. Ceci est du à un déséquilibre trop important entre les neutrons et protons dans le noyau.
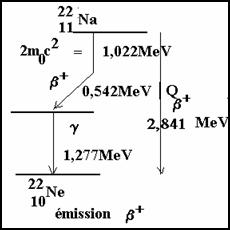
3-2-1.1 émission b +
La particule b+ est un positon, car il y a trop de protons dans le noyau.
![]()
On peut considérer que c’est un proton qui se transforme en un neutron
![]()
n est un neutrino de charge nulle et de masse vraisemblablement nulle.
exemple :
![]()
3-2-1.2 émission b -
La particule b- est un électron expulsé du noyau. Il y a émission d'un antineutrino, pour conservation de l'énergie. On peut considérer que b- correspond à la transformation d’un neutron en proton, car il y a un excès de neutron dans le noyau.
![]()
exemple :
![]()
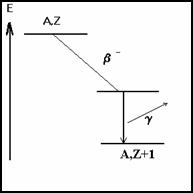
3-2-1.3 Diagramme d’énergie
Les particules b ont une énergie qui n’est pas quantifiée. Mais le nombre de positon ou électron est maximum pour une énergie de 0,58 MeV
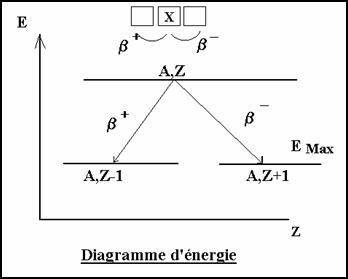
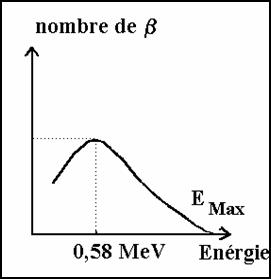
figure 1 figure 2
L’énergie des particules b émis n’est pas constante pour un type de désintégration.
EB ¹ EA,Z - Ea,Z’
Sur un nombre très grand de désintégrations b on observe une répartition d’énergie des particules de la forme de la figure 2. Le maximum de particule a une énergie (EMax) *1/3
On peut déterminer Emax :
Emax + m0c2 = M’(A,Z) c2 - M(A,Z ± 1) c2
où m0 est la masse au repos, de la particule b .On constate que toutes les particules
b n’ont pas la même énergie cinétique. On obtient un spectre continu d’énergie (figure 2).
Par exemple pour le phosphore 32 qui est un émetteur b-
![]()
l’énergie est :
EP = 15 Mp c2 + 17 Mn c2 - B ( B énergie de liaison : binding)
Pour le soufre 32
ES = 16 Mp c2 + 16 Mn c2 - B
L’énergie disponible est E = D E =1.732 MeV
Donc sauf dans le cas rare où l’énergie des b est Emax , il n’y a pas conservation de l’énergie; donc on est obligé de supposer l’existence d’une particule sans masse et sans charge : le neutrino. Son énergie de masse est :
|
|
mn c2 < 10 eV
Le neutrino est une particule très pénétrante, mais non ionisante, qui n’interagit pas avec la matière.
Mais dans de nombreux cas le noyau final est dans un état excité. Il y a libération d’un photon g
On peut écrire :
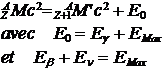
Pour les b+ : si on appelle M’ la masse du noyau, et M la masse de l’atome on peut écrire :
![]()
si on ajoute aux deux membres la masse de Z électrons on obtient :
![]()
Si on appelle Qb+ la différence des masses atomiques des atomes lors de la désintégration b+
![]()
Pour que la désintégration b+ soit énergétiquement possible, il faut que :
Qb+ ≥ 2m0c2 = 2*0,511 MeV = 1,022 MeV
Pour b- il faut que ![]()
Si on ajoute les Z électrons c’est à dire une masse Zm0c2 aux deux membres avec m0 masse de l’électron au repos on obtient :
![]()
![]()
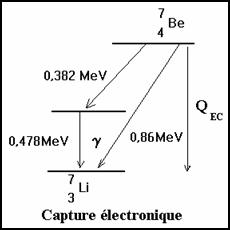
3-2-1.4 Capture électronique
Il peut y avoir au lieu d’une émission d’une particule b+ , une capture électronique avec transformation d’un proton en neutron :
p+ + e- ® n + n
I l y a transformation dans le noyau d’un proton en neutron comme dans l’émission b+ La capture électronique est en concurrence avec l’émission b+ . Le noyau résiduel est laissé dans un état excité, et il y aura émission d’un photon g .
![]()
L’énergie de désintégration est
E0= EM’ +En + Eg » EM’ +Eg
Si on ajoute (Z-1) m0 c2 aux deux membres on obtient :
![]()
E0 = QCE
La capture électronique ne peut se produire que si QCE > 0 c’est à dire si
|
ZM > Z-1 M |
L’émission b+ n’est possible que si ZM > Z-1M + 2m0
Par exemple :
Si Q > 2 m0 c2 la capture électronique est prépondérante devant b+ pour les atomes lourds (Z grand) car les électrons sont en moyenne plus près du noyau.
Après une capture électronique, il y a réarrangement du cortège électronique soit par émission X caractéristique de l’atome fils, soit par émission d’électron Auger.
3-3 Désintégration a
C’est une désintégration non isobarique, avec émission d’un noyau d’Hélium He
![]()
Ma = 4,00150 u
Ma c2 = 3727,41 MeV
Energie de liaison totale B = 28,3 MeV
Energie de liaison par nucléon B/A = 7,07 MeV/nucléon
|
noyau |
2H |
3H |
3He |
4He |
6Li |
7Li |
|
B (MeV) |
2,22 |
8,48 |
7,72 |
28,3 |
32 |
9,2 |
|
B/A |
1,11 |
2,83 |
2,57 |
7,07 |
5,33 |
5,60 |
On peut remarquer que l’énergie de liaison par nucléon est la plus grande pour la particule a donc c’est une particule très stable.
3-3-1 Energie de la désintégration a
Il y a conservation de l’énergie lors de la réaction :
![]()
Ea et EM’ sont les énergies de recul de la particule a et du noyau fils. Si on écrit la conservation de la quantité de mouvement
M’Vr = M’a Va Þ Vr = Va *(M’a/M’)
L’énergie de recul du noyau est :
![]() or
or ![]()
![]()
Les émetteurs
a sont des noyaux lourds A @ 200 donc ![]()
EM’@0,02 Ea et si Ea = 5 MeV EM’@ 100 keV
L’énergie totale ou énergie de désintégration sera :
![]()
![]()
![]()
La désintégration a ne peut donc avoir lieu que si Qa > 0 Þ A > 140
L’énergie de désintégration a varie dans une bande étroite de 4 à 9 MeV. On constate que l’émission a donne plusieurs raies voisines ; on observe une structure fine.
3-3-2 Période des émetteurs a
La période des émetteurs a varie de 10-7 s à 1010 ans.
Plus l’énergie est grande plus la période est courte.
|
Nucléide |
Ea ( MeV) |
Période T |
|
232 Th |
4.05 |
1,39.1010 ans |
|
226 Ra |
4.88 |
1,62.103 ans |
|
228 Th |
5.52 |
1,9 ans |
|
222Rn |
5.59 |
3,83 jours |
|
218 Po |
6.12 |
3,05 min |
|
216 Po |
6.89 |
0,16 s |
|
212 Po |
8.95 |
3.10-7 s |
3-3-3 Noyaux ayant plusieurs modes de désintégration
Certains noyaux ont plusieurs modes possibles de désintégration.
Par exemple :
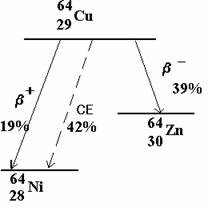
Le 64Cu se désintègre soit par émission b- ou b+ soit par capture électronique CE.
Chaque mode de désintégration est caractérisée par sa probabilité partielle par unité de temps :
lb- lb+ lCE
Chacune de ces probabilités est indépendante. La constante l de désintégration du cuivre 64Cu est :
l = lb- + lb+ + lCE