Vérification d'une théorie approchée relative à une barre chauffée à une extrémité et qui se refroidit par convection naturelle et rayonnement dans l'air ambiant.
Détermination du coefficient d'échange thermique moyen barre - air ambiant.

Soit une barre métallique très allongée de section circulaire constante. Prenons l'origine des abscisses en un point O à priori quelconque et orientons l'axe de la barre par le vecteur unitaire .

La barre est placée dans l'air ambiant ( température Ta ). Un dispositif de chauffage régulé entoure l'extrémité de la barre du côté des x négatifs. A l'intérieur du métal, la chaleur se propage donc vers les x positifs et se dissipe tout au long de la barre dans l'air ambiant, à travers la paroi latérale. On veut étudier la répartition de température à l'intérieur de la barre et pour cela, on adoptera l'hypothèse simplificatrice suivante qui constitue une bonne approximation :
On admet que la température est la même en tous les points d'une section droite ; ainsi en régime stationnaire, la température est une fonction de x seulement. Cette hypothèse est justifiée si la barre est métallique, cad si la haute valeur du coefficient de conduction K assure une homogénéisation latérale de la température. Par contre, pour un matériau peu conducteur, cette hypothèse donnerait une mauvaise approximation.
Remarque : Si la température ne dépend que de x, on n'est cependant pas ramené à un problème de " mur " car, ici, il y a une déperdition latérale de la chaleur.

On va établir une relation qui traduit le bilan des échanges thermiques pour un petit élément de barre compris entre la section d'abscisse x de température T et la section d'abscisse x + dx de température T + dT. Supposons K indépendant de T.

Par la section x, d'aire S, il entre une puissance calorifique :
Par la section x + dx il sort une puissance calorifique :
Par la paroi latérale, en assimilant la température moyenne de la paroi latérale de l'élément à T(x),  il sort une puissance calorifique : h étant le coefficient global d'échange convection et rayonnement et D le diamètre de la barre.

En régime stationnaire, on a nécessairement égalité entre les puissances calorifiques qui entrent et celles qui sortent de l'élément ; on arrive à l'équation différentielle suivante :

mais puisque : et en prenant q = T-T_a    

La solution générale de cette équation différentielle est de la forme : q (x) = A₁ exp(S₁.x) + A₂ exp(S₂.x)

A₁ et A₂ étant deux constantes à déterminer à partir des conditions aux limites :
Pour x = + L (extrémité vers x>0) la température T(L) » Ta ( barre "longue").
Pour x = 0 la température est T₀.

En déduire la solution sous la forme :  

On mesurera T(x) en différents points de la barre de conductivité K connue et on vérifiera la forme exponentielle de la loi T(x) - Ta et on déterminera h.

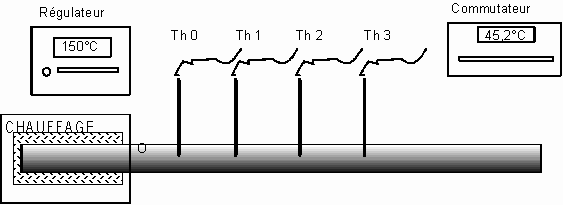 La barre d'aluminium est chauffée à une extrémité. Elle est percée latéralement de trous où logent les couples thermoélectriques.

Par programmation d’une centrale de mesures , enregistrer les températures des quatre premiers thermocouples en fonction du temps. L'instant de départ sera celui de la mise en marche du régulateur du four ; choisir un intervalle de temps de 30 s ou 1 min environ et ceci pendant une vingtaine de minutes.
Mettre en évidence l'établissement du régime stationnaire au sein de la barre en représentant les variations de T₁(t), T₂, T₃ et T₄ . Quelles conclusions peut-on tirer de ces courbes?
Rem : En modifiant la température du four de façon périodique, il est possible de suivre les variations de température le long de la barre .

Lorsque le régime permanent est atteint, relever Ta ainsi que T₀ , T₁ , T₂ , ... T₈ .
Tracer la courbe représentative de (Tx-Ta/T₀-Ta) = f(x). Modéliser selon la solution de l'équation différentielle.
Ce modèle est-il en accord avec la théorie proposée ?
En déduire la valeur de h connaissant K_Al = 230 W.m^-1.K^-1.

Etudier la variation de ce coefficient lorsqu'on modifie les conditions expérimentales par exemple en introduisant un ventilateur le long de la barre.

retour CIRA