Un fluide peut être considéré comme étant formé d'un grand nombre de particules matérielles, très petites et libres de se déplacer les unes par rapport aux autres. Un fluide est donc un milieu matériel continu, déformable, sans rigidité et qui peut s'écouler. Parmi les fluides, on fait souvent la distinction entre liquides et gaz.

1.1 Liquides et gaz :

Les liquides et gaz habituellement étudiés sont isotropes, mobiles et visqueux. La propriété physique qui permet de faire la différence entre les deux est la compressibilité.

q l'isotropie assure que les propriétés sont identiques dans toutes les directions de l'espace.

q la mobilité fait qu'ils n'ont pas de forme propre et qu'ils prennent la forme du récipient qui les contient.

q la viscosité caractérise le fait que tout changement de forme s'accompagne d'une résistance (frottements).

1.2 Forces de volume et forces de surface.

Comme tout problème de mécanique, la résolution d'un problème de mécanique des fluides passe par la définition du système matériel S, particules de fluide à l'intérieur d'une surface fermée limitant S. A ce système on applique les principes et théorèmes généraux de mécanique et thermodynamique :

q principe de la conservation de la masse.

q principe fondamental de la dynamique.

q principe de la conservation de l'énergie.

2 STATIQUE DES FLUIDES

2.1 La grandeur PRESSION :

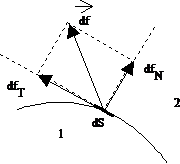
Définition de la pression:

Dans un milieu quelconque, donc aussi dans un milieu fluide, la force que la partie (1) exerce sur la partie (2) à travers un élément de surface réel ou fictif dS a une direction quelconque. Mais cette force peut toujours être décomposée en :

- une composante tangentielle df_T

- une composante normale df_N^.

La quantité df_T /dS représente la contrainte tangentielle et df_N /dS la contrainte normale.

Par définition on appelle Pression la contrainte normale :

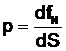
Unité: Le Pascal (Pa) [p] = M L^-1T^-2 .

Remarque : En statique des fluides, seules interviennent les forces de pression df_N, normales à l'élément dS.

Les forces tangentielles df_T n'apparaissent qu'en dynamique des fluides : elles correspondent aux frottements visqueux des couches fluides en mouvement les unes par rapport aux autres et par rapport à la paroi de la conduite.

Pression en point d'un fluide :

En tout point d'un fluide existe une certaine pression. Soit un point M dans un fluide. Si on considère une surface imaginaire dS passant par M, la résultante de toutes les forces dues aux chocs sur dS des particules de fluides en mouvement désordonné est perpendiculaire à cette surface dS et on peut écrire :

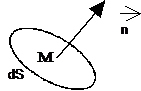
étant le vecteur unitaire de la normale à dS orienté vers l'extérieur.

Cette force df dépend évidemment de la surface dS envisagée, mais la pression pM au point M du fluide ne dépend pas de dS.

2.2 Principe Fondamental de la Statique des Fluides

Soit un élément de volume de fluide dV se trouvant au point M. Il est soumis à des forces de pression exercées par les parties voisines du fluide. Si le fluide est en équilibre, les forces force de frottement sont nulles. L'élément de volume dV n'est alors soumis, généralement, qu'à son poids et aux forces de pression.

La condition d'équilibre de cet élément de fluide permet d'écrire l’équation fondamentale de la « Statique des Fluides »:

Expression différentielle de la relation fondamentale :

Dans un repère (l'axe Oz orienté vers le haut) et dans le champ de pesanteur, , l’expression différentielle de la relation fondamentale de la statique des fluides s'écrit :

Cas des fluides isovolumes :

Dans le cas d'un liquide, (ou pour un gaz dans lequel la variation de pression est faible), la masse volumique r ne dépend pas de la pression. De plus, si on suppose la température uniforme, la masse volumique sera considérée comme constante. D'autre part, pour des différences d'altitude courantes, l'accélération de la pesanteur g peut aussi être considérée constante. Dans ce cas on peut intégrer la relation précédente :

ou encore soit :

Conclusions :

- Dans un fluide la pression croît de haut en bas.

- les surfaces isobares sont des plans horizontaux.

- la surface de séparation entre deux fluides non miscibles est un plan horizontal.

Pression absolue et pression relative ou effective :

La pression absolue est une grandeur essentiellement positive (nulle à la limite).

La pression relative est mesurée par rapport à la pression atmosphérique pat : elle est égale à p1 - pat ; elle peut être positive (surpression) ou négative (dépression).

Unités de pression :

Dans le système international, l'unité légale est le pascal (Pa). Mais dans la pratique on utilise des unités dérivées du pascal, ou des unités liées à la méthode de mesure des pressions.

1 bar = 10⁵ Pa 1 mbar = 10^-3 bar = 100 Pa = 1 hPa

D'autre part en divisant tous les termes de la relation de l'hydrostatique par la quantité .g on obtient :

On exprime souvent les pressions en hauteur de colonne de fluide (mCF).

Ex : Pression atmosphérique normale :

p₀= 760 mm Hg = 101 325 Pa » 1 013 mbar.

Remarque : on rencontre encore certaines unités ne faisant partie d'aucun système :

L'atmosphère (atm) correspond à la pression d’une colonne de 760 mm de mercure (Hg).

Le Torr correspond à la pression d’une colonne de 1 mm Hg (soit 133,3 Pa)

Le Psi (pound square inch) correspond à 6,895 x 10³ Pa.

Applications : Mesures des pressions, calcul des forces pressantes s'exerçant sur une surface plane ou gauche.

Grandeurs physiques utilisées :

: masse volumique (M L^-3 ). g : accélération de la pesanteur (LT^-2 )

p : pression statique (M L^-1T^-2 ) F Force (M L T^-2 )

Notion de pression dans une conduite :

Lorsque la conduite est cylindrique notamment, on admettra que la répartition des pressions est hydrostatique dans une section droite.

On peut donc brancher des tubes piézométriques ; ils mesurent par rapport au plan de référence la quantité :

3 TENSION SUPERFICIELLE

3.1 Le phénomène

Observations

· La surface libre de l'eau dans un tube forme un ménisque près des bords.

· Les poils d'un pinceau sec se rassemblent lorsqu'ils sont mouillés.

· Une aiguille fine en acier flotte à la surface de l'eau.

· L'eau monte dans un capillaire alors que le mercure descend.

· Une plaque de verre adhère très fortement à une surface plane lorsque celle-ci est mouillée.

· Une lame de savon prend une forme telle que sa surface soit minimale.

Conclusion

· La surface libre d’un liquide tend à se contracter spontanément de façon à acquérir une aire minimale.

· La surface d’un liquide se comporte un peu comme la membrane tendue d’un ballon.

La force de tension superficielle

3.2 Force de tension superficielle appliquée à un solide tiré par une lame liquide

Considérons un cadre ABCD dont le coté AB, de longueur L, peut glisser sur DA et CB. Plongé initialement dans un liquide (par exemple de l'eau de savon), ce cadre est rempli d'une lame mince liquide. Le liquide tire AB vers DC par une force f sur chaque face de la lame, proportionnelle à la longueur L, telle que f = g·L.

Pour maintenir AB en équilibre, il faut lui appliquer une force F (qui ne dépend pas de la position de AB) telle que F = 2·f ou

avec F en N , L en m et g en N·m^–1.

Définition

Dans la relation précédente, le coefficient g s'appelle tension superficielle du liquide.

Dimension : [g] = M T^-2.

Unité : Dans le système international (SI), l'unité de tension superficielle n'a pas de nom particulier : (N·m^–1).

Ordres de grandeur (dans le cas d'interface liquide-air)

Liquide	g (N·m^–1) à 20 °C
eau (à 20 °C	73 x·10^–3
eau (à 0 °C)	75,6 x×10^-3
huile végétale	32 x·10^–3
Ethanol	22 x·10^–3
Ether	17 x·10^–3
Mercure	480 x·10^–3

Angle q de raccordement liquide/solide

Une goutte de liquide déposée sur une plaque solide plane et horizontale peut :

· soit s'étaler largement (par exemple de l'eau sur du verre propre) ; dans ce cas, on dit que le liquide mouille parfaitement le solide, et l'angle de raccordement q vaut 0°,

· soit former une lentille :

· si q < 90°, le liquide mouille imparfaitement le solide (par exemple l'eau sur du verre sale)

· si q > 90°, le liquide ne mouille pas le solide (par exemple le mercure sur du verre).

Le même angle de raccordement se retrouve à la surface libre d'un liquide près des bords du récipient et provoque la formation d'un ménisque dans les tubes.

(exemples de l’eau et du mercure)

3.3 Tube capillaire - loi de Jurin

Un tube capillaire (du latin capillus : cheveu) est un tube de petit diamètre intérieur.

Lorsqu'on plonge un tube capillaire, ouvert aux deux extrémités, dans un liquide, celui-ci "monte" (si q < 90 °) ou "descend" (si q > 90 °) dans le tube d'une hauteur h telle que :

r : rayon intérieur du tube

r : masse volumique du liquide

g : intensité de la pesanteur

g : tension superficielle du liquide

q : angle de raccordement liquide/solide

3.4 Mesurages de tension superficielle

Méthode du capillaire

On applique la loi de Jurin. On mesure la dénivellation h et connaissant les autres paramètres, on en déduit une valeur de g.

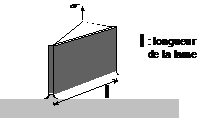
Méthode de la lame immergée ou de l'anneau immergé

Une lame de platine, parfaitement propre, de longueur L, plongée dans un liquide de tension superficielle g, est soutenue par le levier d'une balance de torsion qui permet de mesurer la force F exercée sur la lame (le zéro est réglé lorsque la lame est dans l'air). On soulève doucement la lame jusqu'à ce qu'elle affleure le liquide (la poussée d'Archimède est alors nulle) et on mesure alors la force F = 2·g·L . On en déduit une valeur de g.

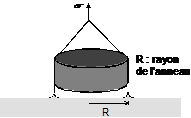
La lame peut être remplacée par un anneau de rayon R, soutenu par un dynamomètre. On soulève lentement l'anneau et, au moment de son arrachement de la surface du liquide, on mesure la force F = 4·p·R·g· . On en déduit une valeur de g.

Méthode du stalagmomètre

Lorsqu'un liquide, de masse volumique r, s'écoule par un tube fin, le poids des gouttes obtenues est proportionnel à la tension superficielle g du liquide et au rayon extérieur R du tube : m·g = k·R·g

On compte le nombre N de gouttes qui s'écoulent pour un volume V donné délimité par deux traits de jauge gravés sur le tube. : N = V·r·g /(k·R·g)

Le stalagmomètre est étalonné avec de l'eau pure à 20 °C : N₀ = V·r₀·g/(k R·g₀)

On obtient :

Applications : agents tensioactifs

Le rôle des agents tensioactifs est d'abaisser la valeur de la tension superficielle des liquides dans lesquels ils sont ajoutés pour les rendre mouillants, moussants, détergents, émulsifiants...

4 DYNAMIQUE DES FLUIDES INCOMPRESSIBLES

4.1 DEFINITIONS :

Le DEBIT est la quantité de matière qui traverse une section droite de la conduite pendant l'unité de temps.

Débit masse :

Si dm est la masse élémentaire de fluide qui a traversé une section droite de la conduite pendant l’intervalle de temps dt, le débit-masse s’écrit :

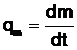unité : kg×s^-1(M T^-1)

Débit volume :

Si dV est le volume élémentaire de fluide qui a traversé une section droite de la conduite pendant l’intervalle de temps dt , le débit-volume s’écrit :

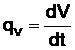unité : m³×s^-1(L³ T^-1)

Relation entre qm et qV : La masse volumique est donnée par la relation :

d'où :

Remarques : Les liquides sont incompressibles et peu dilatables (masse volumique constante) ; on parle alors d'écoulements isovolumes.

Pour les gaz, la masse volumique dépend de la température et de la pression.(L'étude des fluides compressibles sera faite ultérieurement). Pour des vitesses faibles (variation de pression limitée) et pour des températures constantes on retrouve le cas d'un écoulement isovolume.

4.2 Ecoulements PERMANENTS OU STATIONNAIRES :

Un régime d'écoulement est dit permanent ou stationnaire si les paramètres qui le caractérisent (pression, température, vitesse, masse volumique, ..), ont une valeur constante au cours du temps.

4.3 EQUATION DE CONSERVATION DE LA MASSE ou EQUATION DE CONTINUITE

DEFINITIONS :

Ligne de courant : En régime stationnaire, on appelle ligne de courant la courbe suivant laquelle se déplace un élément de fluide.

Tube de courant : Ensemble de lignes de courant s'appuyant sur une courbe fermée.

Filet de courant : Tube de courant s'appuyant sur un élément de surface dS.

La section de base dS du tube ainsi définie est suffisamment petite pour que la vitesse du fluide soit la même en tous ses points (répartition uniforme).

4.4 CONSERVATION DU DEBIT MASSE :

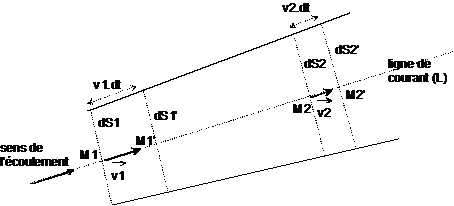
Pendant l'intervalle de temps dt, infiniment petit, la masse dm1 de fluide ayant traversé la section dS1 est la même que la masse dm₂ ayant traversé la section dS₂.

Les volumes correspondants sont égaux à M₁ M₁'. dS₁ et M₂M₂'. dS₂. La conservation de la masse s'écrit :

soit encore :

En régime stationnaire, le débit masse est le même

à travers toutes les sections droites d'un même tube de courant.

Expression en fonction de la vitesse :

La distance MM' s'écrit v dt en fonction de la vitesse du fluide et donc la relation précédente se met sous la forme : soit : ou

Pour un écoulement isovolume ( = Cte) : soit : ou

On retrouve évidemment la relation : dqm = dq_v

Vitesse Moyenne :

En général la vitesse v n'est pas constante sur la section S d'un tube de courant ; on dit qu'il existe un profil de vitesse (forces de frottement). Le débit masse ou le débit volume s'obtient en intégrant le débit élémentaire sur toute la surface S.

Dans une section droite S de la canalisation, on appelle vitesse moyenne vm la vitesse telle que :

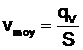
La vitesse moyenne v_moy apparaît comme la vitesse uniforme à travers la section S qui assurerait le même débit que la répartition réelle des vitesses.

Si l'écoulement est isovolume, cette vitesse moyenne est inversement proportionnelle à l'aire de la section droite.

4.5 EQUATION DE CONSERVATION DE L'ENERGIE

THEOREME DE BERNOULLI

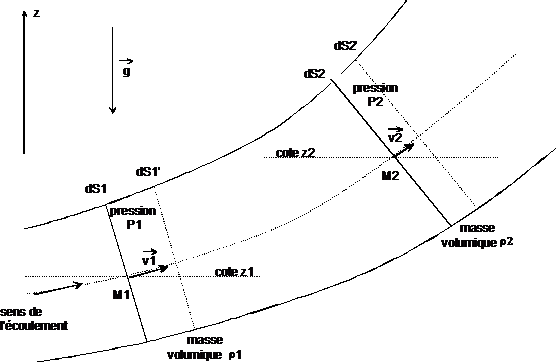
Soit m une masse de fluide parfait (écoulement stationnaire isovolume, pas de frottement) entre les sections dS₁ et dS₂ à l'instant t (schéma ci-dessous); à l'instant t + dt, m se trouve entre dS₁' et dS₂'.

Par application de la conservation de l’énergie, appliquée à cette masse m entre les instants t et t + dt , on montre que l'on peut écrire :

= Cte soit encore :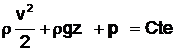

travail des forces de volume (poids) et des forces de surface (pression)

p est la pression statique, est la pression de pesanteur, est la pression cinétique.

En divisant tous les termes de la relation précédente par le produit g, on écrit tous les termes dans la dimension d'une hauteur (pressions exprimées en mètres de colonne de fluide).

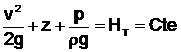( H_T = Hauteur Totale)

= Hauteur de Pression, = Hauteur dynamique, z = Hauteur de position ou côte

= Hauteur piézométrique.

Cas d'un écoulement (1) ® (2) sans échange de travail

Lorsque, dans un écoulement d’un fluide parfait, il n'y a aucune machine (ni pompe ni turbine) entre les points (1) et (2) d'une même ligne de courant, la relation de Bernoulli peut s’écrire sous l'une ou l'autre des formes suivantes :

4.6 RELATION DE BERNOULLI GENERALISEE

Cas d'un écoulement (1)®(2) avec échange d’énergie

Si les forces de frottement interviennent (Pf puissance dissipée < 0) ou lorsque le fluide traverse une machine hydraulique, il échange de l’énergie avec cette machine : la puissance P échangée est :

q P > 0 si l’énergie est reçue par le fluide (ex. : pompe P_G) ;

q P< 0 si l’énergie est fournie par le fluide (ex. : turbine P_R ).

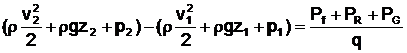
Cas d’une pompe : (voir chapitre Pompes).

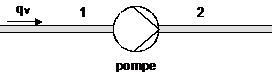
Pour une pompe on appelle Hauteur nette ou Hauteur manométrique la grandeur H donnée par :

ou q_V est le débit volume, q_m est le débit masse

Frottements

Il reste maintenant à établir la puissance dissipée par les forces de frottement ; c'est le calcul des pertes de charge qui sera détaillé dans le chapitre suivant.

4.7 Relation générale

On utilise la relation entre deux points 1 et 2 (le fluide se déplaçant dans le sens 1 2) sous la forme :

Pour une pompe (générateur) :

Pour une turbine (récepteur) :

hi représente toutes les pertes de charge (mCF) entre 1 et 2.

Par ex :

-----------------------------------------------------------------------------------------------------------------------------------------------------

Liens :

Expériences de mécanique des fluides :

http://www.ac-nancy-metz.fr/enseign/physique/Tp-phys/Term/Exp-fluid/exp-flu1.htm

5 VISCOSITE

5.1 Introduction :

Sous l'effet des forces d'interaction entre les molécules de fluide et des forces d'interaction entre les molécules de fluide et celles de la paroi, chaque molécule de fluide ne s'écoule pas à la même vitesse.

On dit qu'il existe un profil de vitesse

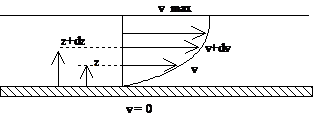
Si on représente par un vecteur, la vitesse de chaque particule située dans une section droite perpendiculaire à l'écoulement d'ensemble, la courbe lieu des extrémités de ces vecteurs représente le profil de vitesse.

Le mouvement du fluide peut être considéré comme résultant du glissement des couches de fluide les unes sur les autres.

La vitesse de chaque couche est une fonction de la distance z de cette courbe au plan fixe : v = v(z).

5.2 Définition de la viscosité dynamique – Loi de Newton :

Considérons 2 couches contiguës distantes de dz.

La force de frottement F qui s'exerce à la surface de séparation de ces deux couches s'oppose au glissement d'une couche sur l'autre. Elle est proportionnelle à la différence de vitesse des couches soit dv, à leur surface S et inversement proportionnelle à dz :

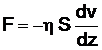
Le facteur de proportionnalité est le coefficient de viscosité dynamique du fluide.

Dimension : [] = M·L^-1·T^-1.

Unité : Dans le système international (SI), l'unité de viscosité est le Pa×s ou Poiseuille (Pl) : 1 Pl = 1 kg×m^-1×s^-1

On trouve encore les tables de valeurs numériques le coefficient de viscosité dans un ancien système d'unités (CGS) : L'unité est le Poise (Po) ; 1 Pl = 10 Po = 1 daPo = 10³ cPo.

Autres unités : La viscosité de produits industriels (huiles en particulier) est exprimées au moyen d'unités empiriques : degré ENGLER en Europe, degré Redwood en Angleterre, degré Saybolt aux USA.

Par rapport aux faits expérimentaux, on est conduit à considérer deux types de fluides :

· D’une part les fluides newtoniens qui satisfont à la loi de Newton. Ces fluides ont un coefficient de viscosité indépendant du gradient de vitesse. C’est le cas des gaz, des vapeurs, des liquides purs de faible masse molaire.

· D’autre part les fluides non-newtoniens. Ce sont les solutions de polymères, les purées, les gels, les boues, le sang, la plupart des peintures, etc … L’étude de ces fluides relève de la rhéologie : fluides pseudo plastiques, rhéoplastiques, thixotropiques, rhéopectiques.

5.3 Viscosité cinématique :

Dans de nombreuses formules apparaît le rapport de la viscosité dynamique et de la masse volumique .

Ce rapport est appelé viscosité cinématique : Dimension : [] = L²·T^-1.

Unité : Dans le système international (SI), l'unité de viscosité n'a pas de nom particulier : (m²/s).

Dans le système CGS, l'unité est le Stoke (St) : 1 m²/s = 10⁴ St.

5.4 Influence de la température :

La viscosité des liquides diminue beaucoup lorsque la température augmente.

Ainsi pour l'eau : à 10°C = 1,3 x 10^-3 Pl

à 20°C = 1,0 x 10^-3 Pl

à 90°C = 0,3 x 10^-3 Pl

Il n'existe pas de relation rigoureuse liant et T. On peut cependant utiliser un modèle utilisant l'équation empirique de Guzman-Andrade de la forme :

a et b étant des constantes dépendant de la nature du liquide et T la température absolue.

Contrairement à celle des liquides, la viscosité des gaz augmente avec la température.

6 DYNAMIQUE DES FLUIDES VISQUEUX INCOMPRESSIBLES

6.1 Rappels : Les différents régimes d'écoulement : nombre de Reynolds

Les expériences réalisées par Reynolds (1883) lors de l'écoulement d'un fluide dans une conduite cylindrique rectiligne, ont montré l'existence de deux régimes d'écoulement : laminaire et turbulent.

En utilisant des fluides divers (viscosité différente), en faisant varier le débit et le diamètre de la canalisation, Reynolds a montré que le paramètre qui permettait de déterminer si l'écoulement est laminaire ou turbulent est un nombre sans dimension appelé nombre de Reynolds et donné par :

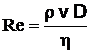ou 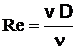avec :

= masse volumique du fluide, v = vitesse moyenne, D = diamètre de la conduite

= viscosité dynamique du fluide, = viscosité cinématique

L'expérience montre que :

si Re < 2000 le régime est LAMINAIRE

si 2000 < Re < 3000 le régime est intermédiaire

si Re > 3000 le régime est TURBULENT

Ces valeurs doivent être considérées comme des ordres de grandeur, le passage d'un type d'écoulement à un autre se faisant progressivement.

6.2 Visualisation de l’écoulement

http://www.ac-nancy-metz.fr/enseign/physique/Tp-phys/Term/Reynolds/Reynolds3.htm

7 Calcul des Pertes de Charge

Lorsqu'on considère un fluide réel, les pertes d'énergie spécifiques ou bien comme on les appelle souvent, les pertes de charge dépendent de la forme, des dimensions et de la rugosité de la canalisation, de la vitesse d'écoulement et de la viscosité du liquide mais non de la valeur absolue de la pression qui règne dans le liquide.

La différence de pression p = p₁ - p₂ entre deux points (1) et (2) d'un circuit hydraulique a pour origine :

ü Les frottements du fluide sur la paroi interne de la tuyauterie ; on les appelle pertes de charge régulières ou systématiques.

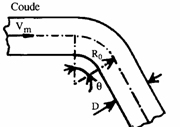
ü La résistance à l'écoulement provoquée par les accidents de parcours (coudes, élargissements ou rétrécissement de la section, organes de réglage, etc...) ; ce sont les pertes de charge accidentelles ou singulières.

Le problème du calcul de ces pertes de charge met en présence les principales grandeurs suivantes :

Le fluide caractérisé par : - sa masse volumique r.

- sa viscosité cinématique n.

Un tuyau caractérisée par : - sa section (forme et dimension) en général circulaire (diamètre D).

- - sa longueur L.

- sa rugosité k (hauteur moyenne des aspérités de la paroi).

Ces éléments sont liés par des grandeurs comme la vitesse moyenne d'écoulement v ou le débit q et le nombre de Reynolds Re qui joue un rôle primordial dans le calcul des pertes de charge.

7.1 PERTES DE CHARGE ACCIDENTELLES

Ainsi que les expériences le montrent, dans beaucoup de cas, les pertes de charge sont à peu prés proportionnelles au carré de la vitesse et donc on a adopté la forme suivante d'expression :

Différence de pression (Pa).

Perte de charge exprimée en mètres de colonne de fluide (mCF)

K est appelé coefficient de perte de charge singulière (sans dimension).

La détermination de ce coefficient est principalement du domaine de l'expérience.

7.2 PERTES DE CHARGE SYSTEMATIQUES

7.2.1 Généralités :

Ce genre de perte est causé par le frottement intérieur qui se produit dans les liquides ; Il se rencontre dans les tuyaux lisses aussi bien que dans les tuyaux rugueux.

Entre deux points séparés par une longueur L, dans un tuyau de diamètre D apparaît une perte de pression p. exprimée sous la forme suivante :

Différence de pression (Pa)

Perte de charge exprimée en mètres de colonne de fluide (mCF)

Perte de charge linéique (m/m)

est un coefficient sans dimension appelé coefficient de perte de charge linéaire.

Le calcul des pertes de charge repose entièrement sur la détermination de ce coefficient .

7.2.2 Cas de l'écoulement laminaire : Re < 2000

Dans ce cas on peut montrer que le coefficient est uniquement fonction du nombre de Reynolds Re ; l'état de la surface n'intervient pas et donc ne dépend pas de k (hauteur moyenne des aspérités du tuyau), ni de la nature de la tuyauterie.

avec

Il est alors immédiat de voir que h est proportionnel à la vitesse v et donc au débit q, ainsi qu'à la viscosité cinématique .

Loi de Poiseuille

Pour un écoulement laminaire, dans une conduite cylindrique horizontale, de longueur L, de rayon r (diamètre D), le débit-volume du fluide est donné par :

7.2.3 Cas de l'écoulement turbulent : Re > 3000

Les phénomènes d'écoulement sont beaucoup plus complexes et la détermination du coefficient de perte de charge résulte de mesures expérimentales. C'est ce qui explique la diversité des formules anciennes qui ont été proposées pour sa détermination.

En régime turbulent l'état de la surface devient sensible et son influence est d'autant plus grande que le nombre de Reynolds Re est grand. Tous les travaux ont montré l'influence de la rugosité et on s'est attaché par la suite à chercher la variation du coefficient en fonction du nombre de Reynolds Re et de la rugosité k du tuyau.

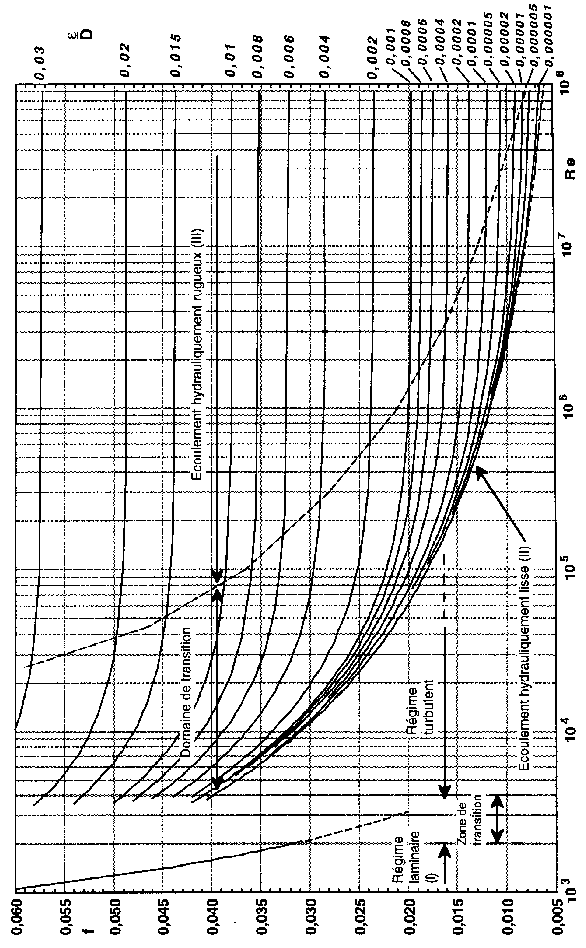
La formule de Colebrook est actuellement considérée comme celle qui traduit le mieux les phénomènes d'écoulement en régime turbulent. Elle est présentée sous la forme suivante :

L'utilisation directe de cette formule demanderait, du fait de sa forme implicite, un calcul par approximations successives ; on emploie aussi en pratique des représentations graphiques (abaques – voir annexe 1).

Résolution de l’équation de Colebrook :

http://www.ac-nancy-metz.fr/enseign/physique/PHYS/Bts-Cira/bts-cira.htm

Pour simplifier la relation précédente, on peut chercher à savoir si l'écoulement est hydauliquement lisse ou rugueux pour évaluer la prédominance des deux termes entre parenthèses dans la relation de Colebrook.

Ce sont les formules de Karman-Nikuradse écrites séparément :

Ec turbulent lisse Ec turbulent rugueux

Remarques :

On fait souvent appel à des formules empiriques plus simples valables pour des cas particuliers et dans un certain domaine du nombre de Reynolds.

Formule de Blasius : (pour des tuyaux lisses et Re < 105)

Formule de Nikuradse ( 10⁶ < Re < 10⁸ )

Formule de Darcy (conduites en fonte) :

J = pertes de charge linéaire (mCF/m)

Bien d'autres relations sont utilisées dans le cas de l'eau :

formule de Williams et Hazen (USA), formule de Strickler (EDF).

Comme en régime laminaire, le régime turbulent ne s'établit parfaitement qu'à partir d'une certaine longueur l qui dans ce cas a pour valeur approximative : .

Pour de grandes valeurs de Re, l'influence de cette longueur ne peut être sensible que pour des tuyaux courts.

On voit donc que des formules empiriques ou des abaques sont utilisées pour avoir des ordres de grandeur corrects des pertes de charge: il est bien entendu que des calculs très précis sont inutiles, car les installations sont toujours dimensionnées avec un coefficient de sécurité permettant une adaptation à des fonctionnements imprévus.

En conclusion, pour diminuer l'ensemble des pertes de charge dans une canalisation, afin de diminuer les coûts de fonctionnement dus aux pompes, il faut:

. diminuer la longueur de canalisation
. diminuer le nombre d'accidents sur la canalisation
. diminuer le débit de circulation
. augmenter le diamètre des canalisations
. faire circuler des liquides le moins visqueux possible
. utiliser des matériaux de faible rugosité

Il est néanmoins évident que le procédés de fabrication impose parfois des contraintes d'ordre supérieur (viscosité élevée des produits utilisés, débits forts imposés...).

Calcul d’une installation hydraulique voir le chapitre « pompes

7.3 Annexe : Abaques

Annexe 1

Annexe 2 : Abaques de Colebrook

8 Théorème d'Euler

8.1 Introduction :

Le théorème de Bernoulli est d'une utilisation trop limitée. En effet, il ne permet pas d'exprimer les actions mécaniques pouvant apparaître entre des fluides et des solides par exemple. D'où la nécessité d'introduire un deuxième théorème.

Dans ce qui suit on considérera un fluide parfait (incompressible, non visqueux) et un écoulement stationnaire.

8.2 Théorème d'Euler :

On établit le théorème d'Euler à partir de la relation fondamentale de la dynamique :

est la quantité de mouvement du système et la somme des forces extérieures appliquées au système.

On considère un tube de courant. On délimite une partie du fluide par une surface fermée (surface de contrôle) ; la représentation de cette surface permet de définir le système.

En calculant la variation de la quantité de mouvement entre les instants t et t + dt, on montre que :

q_m est le débit masse du fluide.

v₁ et v₂ sont les vitesses moyennes dans les sections S₁ et S₂.

représente les forces de volume (poids) et l'ensemble des forces de surface (pression).

8.3 Application du théorème d'Euler :

Définir le système par une surface de contrôle convenable.

Faire le bilan des forces et appliquer la relation précédente.

Résoudre par une méthode graphique ou par projection.

Remarques :

- La surface fermée (contrôle) est toute entière dans le fluide et ne coupe pas un corps solide. Elle est limitée en général par 2 sections et les parois de la canalisation.

- Lorsqu'on fait le bilan des forces on est amené à faire figurer systématiquement le poids du fluide considéré. Or, la surface de contrôle est quelconque et cela pose un problème. On peut régler ce problème de deux façons :

* Soit on peut négliger le poids (grands débits, faibles sections).

* Soit on effectue les projections de l'équation vectorielle dans un plan horizontal.

9 LES POMPES

9.1 Introduction

Les pompes sont des appareils permettant un transfert d’énergie entre le fluide et un dispositif mécanique convenable. Suivant les conditions d’utilisation, ces machines communiquent au fluide soit principalement de l’énergie potentielle par accroissement de la pression en aval, soit principalement de l’énergie cinétique par la mise en mouvement du fluide.

L’énergie requise pour faire fonctionner ces machines dépend donc des nombreux facteurs rencontrés dans l’étude des écoulements :

· Les propriétés du fluide : masse volumique, viscosité, compressibilité.

· Les caractéristiques de l’installation : longueur, diamètre, rugosité, singularités …

· Les caractéristiques de l’écoulement : vitesse, débit, hauteur d’élévation, pression …

Devant la grande diversité de situations possibles, on trouve un grand nombre de machines que l’on peut classer en deux grands groupes :

q Les pompes volumétriques comprenant les pompes alternatives (à piston, à diaphragme, …) et les pompes rotatives (à vis, à engrenage, à palettes, hélicoïdales, péristaltiques …).

q Les turbo-pompes sont toutes rotatives ; elles regroupent les pompes centrifuges, à hélice, hélico-centrifuges.

9.2 Caractéristiques générales des pompes centrifuges.

Une pompe centrifuge est une machine tournante destinée à communiquer au liquide pompé une énergie suffisante pour provoquer son déplacement dans un réseau hydraulique comportant en général une hauteur géométrique d‘élévation de niveau (Z), une augmentation de pression (p) et toujours des pertes de charges.

Une pompe centrifuge est constituée principalement par une roue à ailettes ou aubes (rotor) qui tourne à l’intérieur d’un carter étanche appelé corps de pompe.

Pour améliorer le rendement de la pompe, on peut intercaler entre le rotor et la volute une roue fixe appelée diffuseur qui est munie d’aubes de courbure convenable.

Le calcul des pompes centrifuges s’effectue par l’analyse dimensionnelle et par le théorème d’Euler.

Débit :

Le débit q_v fourni par une pompe centrifuge est le volume refoulé pendant l’unité de temps. Il s’exprime en mètres cubes par seconde (m³ /s) ou plus pratiquement en mètres cubes par heure (m³/h).

Hauteur manométrique :

On appelle Hauteur manométrique H d’une pompe, l’énergie fournie par la pompe à l’unité de poids du liquide qui la traverse. Si H_TA est la charge totale du fluide à l’orifice d’aspiration et H_TR la charge totale du fluide à l’orifice de refoulement, la hauteur manométrique de la pompe est : H = H_TA - H_TR

La hauteur varie avec le débit et est représentée par la courbe caractéristique H = f(q_v) de la pompe considérée.

Rendement :

Le rendement h d’une pompe est le rapport de la puissance utile P (puissance hydraulique) communiquée au liquide pompé à la puissance absorbée P_a par la pompe (en bout d’arbre) ou par le groupe (aux bornes du moteur). Si q_v est le débit volume du fluide, r sa masse volumique et H la hauteur manométrique de la pompe, la puissance P et le rendement h sont donnés par :

Le rendement de la pompe varie avec le débit et passe par un maximum pour le débit nominal autour duquel la pompe doit être utilisée ( voir courbe h = f(q_v)._.ci-après).

9.3 Limitation de la hauteur manométrique d’aspiration - NPSH (1) ; Cavitation

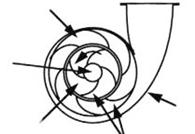
La cavitation est la vaporisation du liquide contenu dans la pompe quand il est soumis à une pression inférieure à la tension de vapeur correspondant à sa température.

Ce phénomène se produit à l’orifice d’aspiration de la pompe ; des bulles apparaissent dans les zones où la pression est la plus faible (entrée des aubes de roue des pompes centrifuges) : elles sont transportées dans les zones de pressions plus fortes où se produit leur recondensation. Des implosions se produisent alors à des fréquences élevées et créent des surpressions locales très élevées (jusqu'à des centaines de bars)

La cavitation est un phénomène à éviter absolument, car il entraîne de graves conséquences:

ü érosion du matériau pouvant aller jusqu'au perçage des aubes de turbine des pompes centrifuges

ü augmentation du bruit et des vibrations générés par la pompe

ü chute des performances des pompes avec diminution importante de la hauteur manométrique totale, du débit et du rendement.

http://www.ac-nancy-metz.fr/enseign/physique/PHYS/Bts-Cira/cavitation/cavitation.htm

Le critère qui sert à définir la pression nécessaire à l’aspiration pour obtenir un bon fonctionnement de la pompe, cad pour maintenir en tout point du fluide une pression supérieure à la pression de vapeur saturante, est le « ‘NPSH » (sigle de l’abréviation anglo-saxonne de « Net Positive Suction Head » over vapour pressure).

Cette caractéristique, donnée par le constructeur est qualifiée de « NPSH requis ». Elle tient compte en particulier de la chute de pression que subit le fluide lors de son accélération à l’entrée de la roue.

La pompe ne fonctionnera correctement que si la pression totale à l’entrée p_A est supérieure à la somme p° + NPSH requis. On appelle « NPSH disponible » la différence entre la pression totale à l’entrée et la pression de vapeur saturante :

Pour qu’une pompe fonctionne normalement (sans cavitation), il faut que le NPSH disponible (calculé) soit supérieur au NPSH requis (indiqué par le constructeur).

NPSH disponible > NPSH requis

Les conditions d’aspiration sont d’autant meilleures que la différence entre les deux est grande.

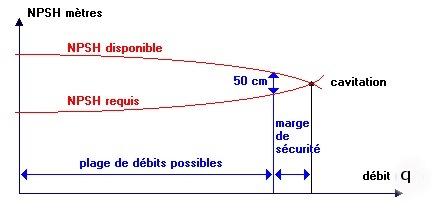
En conclusion, on peut dresser une liste de conseils à respecter, si le procédé le permet, pour éviter la cavitation:

. préférer si possible les montages de pompes en charge.

. éviter de transporter des liquides à des températures trop élevées.

. éviter une alimentation à partir d'un réservoir sous pression réduite.

. diminuer les pertes de charge du circuit d'aspiration.

Si ces conseils ne peuvent être appliqués en raison des exigences du procédé, il ne reste plus qu'à trouver une pompe dont les caractéristiques montrent des valeurs de N.P.S.H.requis suffisamment faibles.

9.4 Caractéristiques

Les résultats indiquent comment la hauteur manométrique H_m, la puissance P_a et le débit q varient en fonction des paramètres (vitesse et diamètre du rotor, nature du fluide, …).

En particulier, la hauteur H ne dépend pas de la masse volumique du fluide (application à l’amorçage des pompes centrifuges).

Ci-contre les variations de H en fonction de la vitesse de rotation.

Ci-dessous, les caractéristiques en fonction du modèle choisi.

Pompe en aspiration Pompe en charge

10 Courbe de réseau

Courbe représentative des pertes de charge en fonction du débit

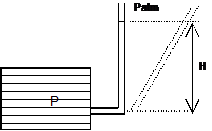
Considérons l’installation ci-dessous :

En appliquant la relation de Bernoulli généralisée, on peut exprimer la hauteur manométrique H de la pompe sous la forme :

soit

En négligeant les termes de vitesse et en supposant p₁ = p₂

Les pertes de charge H_j1 +H_j2 dans la conduire d’aspiration (1) et dans la conduite de refoulement (2) sont données par la somme des pertes de charge singulières et des pertes de charge systématiques :

Si l’écoulement est turbulent rugueux, l est une constante et donc les pertes de charge sont proportionnelles à q².Dans le cas d’un écoulement turbulent lisse (l = 0,316.Re^-025 relation de Blasius), les pertes de charge sont proportionnelles à q^1,75 .

est donc d’allure parabolique et ressemble à la courbe ci-dessous :

Le point de fonctionnement de l’installation se situe à l’intersection de la courbe de réseau et de la caractéristique de la pompe.

Retour vers Mécanique des fluides