1. de transformations infiniment lentes : sans intérêt car dans ce cas le travail fourni serait infiniment petit (l'énergie interne U étant de valeur finie).
2. de transformations cycliques où l'état final et initial sont identiques : c'est ce qui est réalisé en pratique.

2. Les moteurs thermiques dithermes.
On a vu (voir cours n° 5) qu’il fallait absolument 2 sources de chaleur au minimum pour avoir un moteur (un moteur monotherme étant impossible à réaliser). Le moteur ditherme est donc le moteur "minimal" qui échange de la chaleur entre deux sources. Cet échange de chaleur (qui correspond globalement à une absorption de chaleur sur un cycle) permet une perte de travail, c'est - à - dire de l'énergie motrice fournie à l'extérieur.
Les moteurs dithermes prennent de la chaleur Q2 d’un corps chaud pour la convertir en énergie motrice W. Ils perdent cependant une partie de cette chaleur Q1 qu'ils rejettent à la source froide. Ils possèdent donc un rendement défini par

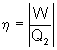
2.1. Le moteur idéal : cycle de Carnot.
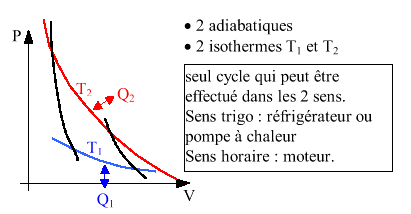
C'est le moteur idéal car il possède le meilleur rendement faisable pour un travail donné. Il est réversible, donc il est forcément composé de 2 isothermes et de 2 adiabatiques qui permettent de passer de l'isotherme chaude T2 à l'isotherme froide T1. Q1 et Q2 sont forcément échangées sur les isothermes puisque les autres transformations n'échangent pas de chaleur. Les sources chaudes et froides sont des thermostats, donc leur température ne varie pas. 

On calcule alors le rendement (voir ½ page de droite). Il s'agit du rendement maximal que l'on peut obtenir avec 2 sources de chaleur données.
Ce résultat montre que le rendement ne dépend pas du fluide et est d'autant + élevé que T1 est faible et T2 élevé
 
 

2.2. Exemple d’un moteur ditherme réel : le cycle de Beau De Rochas (essence).
Un moteur de Carnot est très compliqué (donc très cher) à réaliser, pour des raisons techniques (et non théoriques). On fabrique donc des moteurs plus simples (moins cher) mais non réversibles (donc avec un rendement plus faible ou bien un travail perdu plus faible).

Le moteur vu ici est constitué de 4 temps : un "temps" correspondant à une course totale du piston et non à un type de transformation sur le diagramme P(V). Le fluide utilisé est un mélange air - essence (assimilable à de l'air pur car le volume d'essence est négligeable. )

•  L'admission et la compression sont possibles car le moteur a été préalablement lancé (au moyen d’un moteur électrique) et un volant d'inertie permet d'emmagasiner l'énergie cinétique du lancement pour permettre l'aspiration de l'air. Par la suite, la présence de 3 autres cylindres, chacun fonctionnant sur un temps différent, permet une rotation plus régulière du moteur ainsi qu'un travail fourni 4 fois plus élevé. La compression est nécessaire pour permettre l'explosion du mélange.
•  La détente est provoquée par l'explosion du mélange air-essence qui crée une chaleur intense et très rapide.
•  L'échappement est provoqué par la phase de détente d'un autre piston qui entraîne le vilebrequin.

Seule la phase de détente correspond en fait à l'apport de travail à l'extérieur.
On peut alors observer le cycle dans le plan P(V) : voir ½ page de droite :

• Le fait que l'explosion soit isochore s'explique par le fait que l'explosion du mélange air - essence est très rapide (contrairement à l'explosion d’un mélange air - gasoil des diesel).
•  La compression et la détente sont adiabatiques du fait de la rapidité de la course du piston ( On a 4 temps pour 2 tours, donc à 3000 tr/min le piston effectue 6000 déplacements / min, soit 1 déplacement / 10 ms. Or la chaleur met beaucoup plus de 10 ms à s'évacuer Þ compression et détente adiabatiques.).
• Lors de l'ouverture de la soupape d'échappement, la pression est égale à la pression extérieure (pas de viscosité d’un gaz parfait).
• Pour finir le cycle est considéré comme quasi - statique ; cela se justifie par le fait que la vitesse des molécules d'air est de l'ordre de 700 m/s à 600K, or la course du piston (6 cm par exemple) s'effectue en 10 ms, soit une vitesse de déplacement de 6cm/10ms = 6m/s << 700 m/s du gaz : la pression a donc le temps de s'équilibrer.

 On a le travail obtenu sur un cycle :
W = W₀₁ + W₁₂ + W₂₃ + W₃₄ + W₄₁ + W₁₀, or W₀₁ = -W₁₀, d'où W = W₀₁ + W₁₂ + W₂₃ + W₃₄ + W₄₁ = surface hachurée du cycle ( = W_total du cours n° 3). 

En pratique, le cycle réel est le suivant :

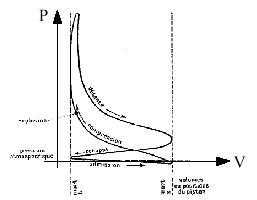
Ce qui signifie que :

1/ l'admission crée une dépression (mélange visqueux)

2/ on provoque l'explosion légèrement avant que le piston n'ait atteint le point mort haut de manière à prendre en compte la durée de l'étincelle et la durée de combustion : c'est l'avance à l'allumage.

3/ La boucle inférieure est décrite dans le sens trigo : cela signifie que le travail fourni est encore plus faible que prévu.

L'exercice présenté à la ½ page de droite donne le calcul théorique du rendement du cycle. En pratique, le rendement effectif est plus faible car le cycle décrit est le cycle réel vu ci-dessus et il y a les frottements des divers organes. On remarque que le rendement est d'autant plus élevé que le taux de compression est élevé (» 6 pour les moteurs à essence).

Ce qui limite t est le phénomène de détonation :  La combustion démarre normalement, mais par suite de l'élévation de pression et de température une autre portion du mélange s'enflamme spontanément. Le cliquetis, caractéristique d'une combustion anarchique, est une onde sonore dont l'énergie provoque une brutale surchauffe pouvant aller jusqu'à la destruction des éléments du cylindre (soupapes, pistons, segments, électrodes de bougie). 

L'indice d'octane permet de limiter le phénomène de détonation, donc augmenter t et h. Les moteurs diesel ne possèdent plus de détonation car il ne s'agit pas d’un gaz explosif que l'on comprime, mais uniquement de l'air. On peut donc encore augmenter t. Ce qui limite t dans ce cas est la pression du gaz qui crée des contraintes mécaniques : t est de l'ordre de 15 et la pression maximale de l'ordre de 50 bars.
 

3. Les machines frigorifiques.
 3.1. Réfrigérateurs.

Ils pompent de la chaleur d’un corps froid et la transmettent à un corps chaud grâce à un compresseur et à un détendeur qui permettent cette opération. Ce cycle nécessite de l'énergie motrice et ne peut donc être parcouru que dans le sens trigonométrique (absorption de travail). On peut calculer le rendement théorique sur l'exemple d’un cycle de Carnot (voir 1/2 page de droite).
L'efficacité est définie par : 

Comme sur une isotherme on a D U = 0 on en déduit que W = - Q Þ sur l'isotherme T₂ ) on a donc Q₂ £ 0 puisque W_T2 ³ 0: la chaleur est rejetée. On démontre de même que sur l'isotherme froide T₁ on a Q₁ absorbée.

Comme ce n'est pas vraiment un calcul de rendement dont il s'agit (car on ne prend en compte que l'énergie W que l'on doit fournir mécaniquement à la pompe et non celle qui est évacuée) on appelle plutôt "efficacité e" le rapport | Q₁/W| .

Un transparent du cours nous montre, de manière très épurée, le principe de lancement de production du froid (intérieur du réfrigérateur initialement à la température ambiante). Cependant, dans tous les exercices abordés en BTS, le cycle de refroidissement est lancé depuis longtemps de sorte que c'est le régime permanent qui est étudié : T_froide et T_chaude sont déjà établies depuis longtemps.
C'est un thermostat qui "lance" le compresseur, et donc les cycles de refroidissement.
 

3.2. Pompes à chaleur.
Il s'agit simplement d’un réfrigérateur ouvert sur l'extérieur qui pompe donc la chaleur Q₁ de l'extérieur et c'est la grille chaude du réfrigérateur qui chauffe la pièce ( Bien évidemment, les pompes à chaleur diffèrent des réfrigérateur non pas au niveau du principe mais au niveau des puissances mises en jeu, diamètre des tuyaux etc). 

Dans ce cas c'est la chaleur Q₂ restituée à l'air ambiant qui nous intéresse, et l’efficacité) est donc définie par :

On démontre alors que pour le cycle de Carnot (le seul réversible) on obtient 

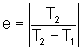
e = 7,5 signifie qu'il est 7,5 fois plus avantageux d'utiliser l'électricité pour alimenter le compresseur de la pompe à chaleur que d'utiliser l'électricité directement pour faire chauffer un radiateur électrique (rendement de 1) !!!
 

Machines thermiques : cycliques pour qu'elles fonctionnent longtemps avec le même gaz.
 

2. Les moteurs thermiques dithermes.

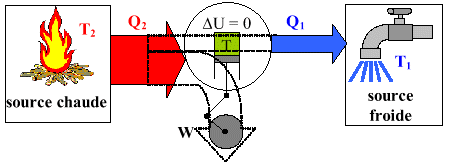
W = -Q₂ - Q₁

Ici T₁ et T₂ sont constantes
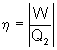avec Q₂ = chaleur prise de la source chaude
 

2.1. Le moteur idéal : cycle de Carnot.

1^er principe : W_cycle = -Q₁ - Q₂ car D U_cycle = 0 
2^nd principe : D S_cycle - (Q₁/T₁ + Q₂/T₂)= 0 car transfo réversible or D S_cycle = 0 Þ Q₁/T₁ + Q₂/T₂ = 0 (résultat fondamental) Û Q₁/Q₂ = -T₁/T₂ 

d'où h = ½ W/Q₂½ = ½ (-Q₂-Q₁)/Q₂½= ½ -1 - Q₁/Q₂½=
½ -1 + T₁/T₂½= 1-T₁/T₂ ainsi :

2.2. Exemple d’un moteur ditherme réel : le cycle de Beau De Rochas (essence).

moteur à essence 4 temps :

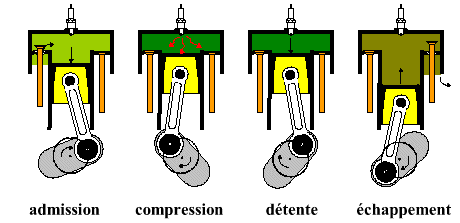
Rotation régulière et augmentation du travail avec 3 autres cylindres qui travaillent chacun sur un temps différent. C'est la détente qui entraîne les 3 autres pistons :

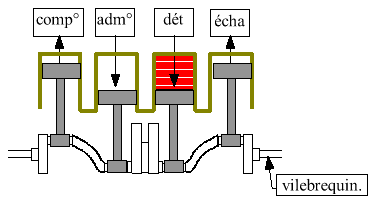
Cycle essence (de Beau de Rochas, ou Otto) :
Explosion très rapide Þ compression isochore
Course des pistons très rapide (6m/s à 3000 tr/min) Þ transfo adiabatique. on a alors :

• 2 adiabatiques.

• 2 isochores (Þ non réversibilité du cycle).

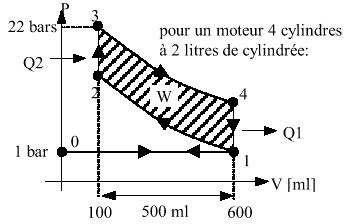
On peut alors observer le cycle dans le plan P(V) :

Explosion très rapide Þ compression isochore
Course des pistons très rapide (6m/s à 3000 tr/min) Þ transfo adiabatique. on a alors :

• 2 adiabatiques.
• 2 isochores (Þ non réversibilité du cycle).

0 ® 1 : admission.
1 ® 2 : compression adiabatique.
2 ® 3 : explosion très rapide ( Þ isochore)
3 ® 4 : détente adiabatique avec production de travail.
4 ® 1 : baisse de pression lors de l'ouverture de la soupape
1 ® 0 : échappement.

De plus T₁.V₁^{g -1} = T₂.V₂^{g -1} et T₃.V₃^{g -1} = T₄.V₄^g-1 
Or V₁ = V₄ et V₂ = V₃ d'où T₃.V₂ = T₄.V₁^{g -1}.
On en déduit que :  T₂ = T₁.(V₁/V₂)^{g -1} = T₁.t ^{g -1}  T₃ = T₄.(V₁/V₂)^{g -1} = T₄.t ^{g -1}
d'où (2) ® Q₁/Q₂ = (T₁ - T₄)/( T₄.t^{g -1} - T₁.t^{g -1}) = (T₁ - T₄)/[t^{g -1} ( T₄ - T₁)] = -t^1-g
 

ainsi (1) ® h = 1 - t 1-g

  h est d'autant plus grand que le taux de compression volumétrique t est élevé.
Ici t = V₁/V₂ = 600/100 » 6 Þh » 51 %
En pratique h » 35 %, voire moins ! 
Rq : ici le 2^nd principe est délicat à écrire car l'explosion n'est pas une source de chaleur (sous - entendu à T = C^te).
 
 

3.1. Réfrigérateurs.

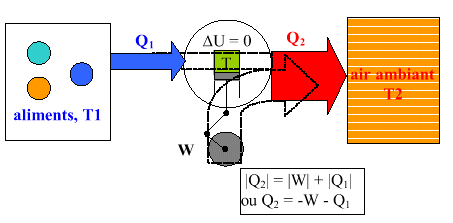
L'efficacité est définie par : e = | Q₁/W|

Cycle de Carnot du frigo.
Il est forcément décrit dans le sens trigo puisque le cycle nécessite de l'énergie motrice pour se réaliser.

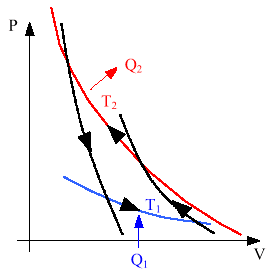
1^er principe Þ W = -Q₁ - Q₂.
2^nd principe : réversible Þ Q₁/T₁ + Q₂/T₂ = 0
Û Q₂ = -Q₁ ´ (T₂/T₁)

e = | Q₁/W| = Q₁/(-Q₂ - Q₁) = Q₁/[Q₁´ (T₂/T₁) - Q₁] 
= Q₁/[Q₁ ´ (T₂/T₁-1)] = 1/(T₂/T₁ - 1) ainsi :
 

e =

pour T₂ » 27 °C (300K) et T₁ » -13 °C (260K) on obtient e » 6,5. La température froide dépend du procédé utilisé (taux de compression etc.)
 

3.2. Pompes à chaleur.

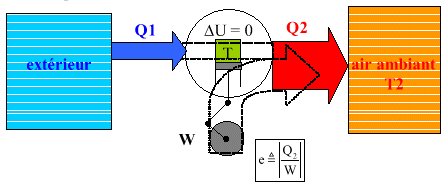
Cycle de Carnot (identique à celui du réfrigérateur) Þ
1^er principe Þ W = -Q₁ - Q₂.
2^nd principe : réversible Þ Q₁/T₁ + Q₂/T₂ = 0.
Û Q₁ = - Q₂´ (T₁/T₂)
 e = | Q₂/W| = Q₂/(-Q₂ - Q₁) = Q₂/[-Q₂ + Q₂.(T₁/T₂)] = Q₂/[Q₂´ (T₁/T₂-1)] = 1/(T₁/T₂ - 1) ainsi 

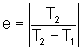
pour T₂ = 27 °C (300K) et T₁ = -13 °C (260K) on obtient e = 7,5. La température chaude dépend du procédé utilisé (taux de compression, méthode de détente etc.). Une pompe à chaleur est d'autant plus efficace que T₁ (température extérieure) est faible.