Un
oscillateur est un système animé d'un mouvement périodique.
Une
masse suspendue à un ressort, un pendule de torsion,
le balancier d'une
horloge, sont des oscillateurs mécaniques
Oscillateurs mécaniquesTerminale STL
Physique de Laboratoire et Procédés IndustrielsMECANIQUE

|
Un
oscillateur est un système animé d'un mouvement périodique.
|
On considère un ressort de masse négligeable et de raideur k.
Á l'une de ses extrémités est fixé un solide (S) mobile de masse m,
l'autre extrémité est accrochée à un point d'un banc horizontal sur lequel
peut se déplacer le solide (S) sans frottement.
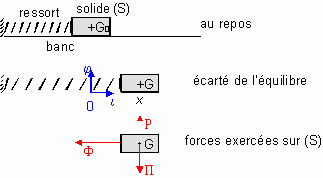
Au repos (le ressort ayant sa longueur naturelle), le solide
(S) est en équilibre sous l'action de son poids et de la réaction du banc : ![]()
Si l'on écarte le centre d'inertie G du solide de sa
position d'équilibre G0 et qu'on le libère, il se met à osciller
autour de G0 ; pour décrire le mouvement de G, on choisira un
repère ![]() lié au banc. Le solide
(S) est soumis à trois forces :
lié au banc. Le solide
(S) est soumis à trois forces :
|
D'après le théorème du centre d'inertie : sur |
L'équation du mouvement de G est donc une équation différentielle du second ordre :
2- Équation horaire
ou
ou
Une solution de l'équation différentielle précédente est : ![]() .
.
En effet en dérivant par rapport au temps t : ![]()
puis en dérivant une seconde fois : ![]()
En reportant x et ![]() dans
l'équation différentielle, on obtient :
dans
l'équation différentielle, on obtient : ![]() ou
ou ![]() soit
soit ![]()
On appelle :
w , T, f et j sont des grandeurs indépendantes de l'amplitude xm du mouvement.
Unitésx et xm en (m), ![]() en (m/s),
en (m/s), ![]() en (m/s²) ,
k en (N/m) ,
m en (kg) , w en (rad/s) , T en (s) ,
f en (Hz) ,j en (rad).
en (m/s²) ,
k en (N/m) ,
m en (kg) , w en (rad/s) , T en (s) ,
f en (Hz) ,j en (rad).
|
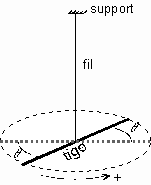
On considère un pendule de torsion constitué d'un fil, de constante de torsion C, et d'une tige fixée en son centre à l'une des extrémités de fil, l'autre extrémité étant fixée à un support. On appelle J le moment d'inertie de la tige par rapport à un axe passant par son centre. Si l'on écarte la tige de sa position d'équilibre et qu'on la libère, elle se met à osciller autour de sa position d'équilibre. On appelle respectivement q et
|
D'après le théorème du moment cinétique, ![]() avec
avec ![]()
L'équation différentielle du second ordre du mouvement de la tige est donc :
![]() ou
ou ![]() ou
ou ![]()
Une solution de l'équation différentielle
précédente est :![]()
On appelle :
Ces grandeurs sont indépendantes de l'amplitude q m du mouvement.
Unités :Remarque :
On appelle oscillateur harmonique un oscillateur dont
le mouvement est déterminé par une équation différentielle du type : ![]()
2- Conservation de l'énergie mécanique d'un oscillateur
1- Cas d'un pendule élastique horizontal
|
On
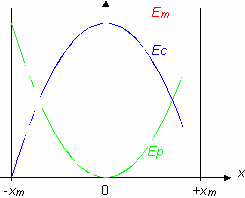
considère le pendule élastique horizontal vu précédemment (M31 § 2). L'équation horaire du mouvement s'écrit : |
L'énergie cinétique du système est ![]() .
.
En prenant pour état de référence la position d'équilibre
(x = 0), l'énergie potentielle du système est ![]() .
.
L'énergie mécanique du système est donnée par ![]()
![]() .
.
![]()
![]()
avec vm : vitesse maximale du solide (lorsqu'il passe à sa position d'équilibre x = 0).
On considère le pendule élastique de torsion vu
précédemment (M31 § 3). Le système est formé du fil de constante de torsion
C et d'une tige fixée en son centre à l'une des extrémités du fil
l'autre extrémité étant fixée à un support. On appelle J le moment
d'inertie de la tige par rapport à un axe passant par son centre. On écarte la
tige de sa position d'équilibre et qu'on la libère. À un instant t
donné, la tige a une abscisse angulaire q et une
vitesse angulaire ![]() .
.
L'équation horaire du mouvement s'écrit : ![]()
et la vitesse angulaire ![]() .
.
L'énergie cinétique du système est ![]() .
.
L'énergie potentielle du système est (en prenant
pour état de référence la position d'équilibre q
= 0) ![]() .
.
L'énergie mécanique du système est donnée par ![]()
![]() . Or
. Or ![]() d'où
:
d'où
:
![]()
![]()
Équation différentielle
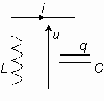
|
Un
circuit L-C peut être le siège d'oscillations électriques. Considérons le circuit formé d'un condensateur parfait de capacité C et d'une bobine parfaite d'inductance L. À un instant t, on appelle i l'intensité dans le circuit et u la tension aux bornes du condensateur selon le schéma ci-contre. |
Par définition de l'intensité : ![]()
La tension aux bornes du condensateur est : ![]()
La tension aux bornes de la bobine est : ![]()
Les tensions u étant égales, le circuit est décrit par l'équation différentielle :
![]()
![]() soit en posant
soit en posant
![]()
![]()
En fonction du temps t :
La charge q du condensateur varie selon l'équation :L'intensité dans le circuit varie selon l'équation : ![]() ,
I étant l'intensité maximale telle que :
,
I étant l'intensité maximale telle que : ![]()
La période des oscillations électrique est : ![]()
L'énergie électrique dans le condensateur est : ![]() .
.
L'énergie électrique dans la bobine est : ![]() .
.
L'énergie électrique totale du circuit est : ![]()
|
pendule |
pendule |
circuit |
|
x |
q |
q |
|
|
|
i |
|
m |
J |
L |
|
k |
C |
1/C |
|
F=- k× x |
G =- C× q |
u= (1/C)× q |
|
Ec = ½ m× |
Ec = ½ J× |
Em = ½ L× i² |
|
Ep = ½ k× x² |
Ep = ½ C× q ² |
Ee = ½ C× u² |
|
Em = ½ k× xm²= ½ m× vm² |
Em = ½ C× |
Non-conservation de l'énergie d'un oscillateur réel
Au cours de ses oscillations, un oscillateur réel
est soumis à des frottements inévitables. Le travail des frottements
(négatif) provoque une diminution de l'énergie mécanique de
l'oscillateur libre pendant son mouvement. On dit alors que l'oscillateur
réel libre est non conservatif. On dit qu'un frottement est fluide lorsque la force de
frottement est proportionnelle à la vitesse : L'étude dynamique d'un pendule élastique horizontal
soumis à ce frottement aboutit à l'équation : Si le frottement est faible, le mouvement est pseudo
périodique. Le système, ayant été écarté de sa position
d'équilibre, oscille, mais l'amplitude des oscillations diminuent
progressivement et leur valeur tend vers 0. L'oscillateur se rapproche
progressivement de sa position d'équilibre. Si le
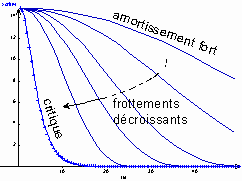
frottement est fort, le mouvement est apériodique. Le système, ayant
été écarté de sa position d'équilibre, revient lentement vers cette
position d'équilibre, mais sans osciller. Ce mouvement est d'autant plus lent
que le frottement est important. En partant d'un frottement fort, si l'on diminue ce
frottement, le mouvement apériodique se fait avec un retour vers la position
d'équilibre de plus en plus rapide. Pour une valeur particulière de ce
frottement, le régime est dit critique : parmi tous les mouvements
apériodiques de cet oscillateur, c'est celui pour lequel le retour vers la
position d'équilibre est le plus rapide. Si, à partir de cette valeur
particulière, on diminuait encore le frottement, le mouvement de
l'oscillateur deviendrait pseudo-périodique Ce régime critique présente un intérêt important
pour les systèmes mécaniques soumis à des vibrations. On désire très
souvent que ces systèmes reviennent rapidement à leur position d'équilibre,
mais sans osciller. La suspension de ces systèmes est donc couplée à des amortisseurs
réglés sur le régime critique (cas des voitures automobile…) On dit qu'un
frottement est solide lorsque la valeur de la force de frottement est constante
(donc indépendante de la vitesse) :
Si l'on veut qu'un oscillateur réel conserve une énergie
mécanique constante, il faut lui fournir un apport régulier d'énergie par
un système extérieur ; on obtient alors un oscillateur entretenu (ce
n'est plus rigoureusement un oscillateur harmonique) ; le système extérieur
peut être, par exemple, les "poids" d'une pendule à balancier, la
roue d'échappement à ancre ou un ressort dans une montre mécanique…![]() ,
le signe moins signifie que le vecteur force est de sens opposé au vecteur
vitesse. Ce type de frottement agit lorsqu'un corps se déplace dans un fluide
(gaz ou liquide).
,
le signe moins signifie que le vecteur force est de sens opposé au vecteur
vitesse. Ce type de frottement agit lorsqu'un corps se déplace dans un fluide
(gaz ou liquide).![]()
L'étude de cette équation différentielle dépasse le
cadre du programme de S.T.L.
Le mouvement de l'oscillateur amorti dépend de
l'importance du coefficient de frottement l
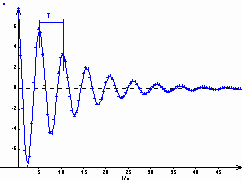
Théoriquement l'équilibre n'est jamais atteint.
![]() .
Le sens du vecteur force est cependant opposé au vecteur vitesse : l'expression
de ce frottement peut donc se mettre sous la forme :
.
Le sens du vecteur force est cependant opposé au vecteur vitesse : l'expression
de ce frottement peut donc se mettre sous la forme : ![]() .
.
Ce type de frottement se produit au contact de deux solides
qui glissent l'un sur l'autre.
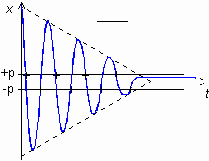
Le mouvement est une suite d'oscillations sinusoïdales de
pulsation w 0
centrées alternativement
sur les abscisses ![]() et
et ![]() .
.
On obtient l'arrêt définitif du mouvement lorsque ![]() s'annule dans la plage [-p,+p]
s'annule dans la plage [-p,+p]