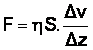GÉNÉRALITÉS
1 - Définition
Un fluide peut être considéré comme étant formé d'un grand nombre de particules matérielles, très petites et libres de se déplacer les unes par rapport aux autres. Un fluide est donc un milieu matériel continu, déformable, sans rigidité et qui peut s'écouler. Parmi les fluides, on fait souvent la distinction entre liquides et gaz.
2 - Liquides et gaz
Les liquides et gaz habituellement étudiés sont isotropes, mobiles et visqueux. La propriété physique qui permet de faire la différence entre les deux est la compressibilité.
· l'isotropie assure que les propriétés sont identiques dans toutes les directions de l'espace.
· la mobilité fait qu'ils n'ont pas de forme propre et qu'ils prennent la forme du récipient qui les contient.
· la viscosité caractérise le fait que tout changement de forme d’un fluide réel s'accompagne d'une résistance (frottements).
3 - Forces de volume et forces de surface
Comme tout problème de mécanique, la résolution d'un problème de mécanique des fluides passe par la définition du système matériel S, particules de fluide à l'intérieur d'une surface fermée limitant S. À ce système on applique les principes et théorèmes généraux de mécanique et thermodynamique :
· principe de la conservation de la masse.
· principe fondamental de la dynamique.
· principe de la conservation de l'énergie.
DYNAMIQUE DES FLUIDES INCOMPRESSIBLES (F1)
1 - DEFINITIONS
Le débit est le quotient de la quantité de fluide qui traverse une section droite de la conduite par la durée de cet écoulement.
1.1 - Débit-masse
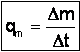 Si Dm est la masse de fluide qui a traversé une
section droite de la conduite pendant le temps Dt,
par définition le débit-masse est : unité : kg·s-1
Si Dm est la masse de fluide qui a traversé une
section droite de la conduite pendant le temps Dt,
par définition le débit-masse est : unité : kg·s-1
1.2 - 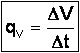 Débit-volume
Débit-volume
Si DV est le volume de fluide qui a traversé une section droite de la conduite pendant le temps Dt, par définition le débit-volume est : unité : m3·s-1.
1.3 - Relation entre qm et qV
La masse volumique est donnée par la relation :
![]() d'où :
d'où : ![]()
Remarques :
Les liquides sont incompressibles et peu dilatables (masse volumique constante) ; on parle alors d'écoulements isovolumes.
Pour les gaz, la masse volumique dépend de la température et de la pression. Pour des vitesses faibles (variation de pression limitée) et pour des températures constantes on retrouve le cas d'un écoulement isovolume.
1.4 - Écoulements permanents ou stationnaires
Un régime d'écoulement est dit permanent ou stationnaire si les paramètres qui le caractérisent (pression, température, vitesse, masse volumique, ...), ont une valeur constante au cours du temps.
2 - Équation de conservation de la masse ou équation de continuité
2.1 - Définitions
 Ligne de
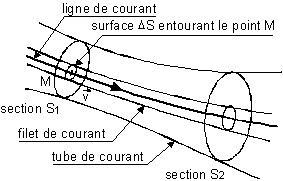
courant : En régime stationnaire, on appelle ligne de courant la courbe
suivant laquelle se déplace un élément de fluide. Une ligne de courant est
tangente en chacun de ses points au vecteur vitesse du fluide en ce point.
Ligne de
courant : En régime stationnaire, on appelle ligne de courant la courbe
suivant laquelle se déplace un élément de fluide. Une ligne de courant est
tangente en chacun de ses points au vecteur vitesse du fluide en ce point.
Tube de courant : Ensemble de lignes de courant s'appuyant sur une courbe fermée.
Filet de courant : Tube de courant s'appuyant sur un petit élément de surface DS.
La section de base DS du tube ainsi définie est suffisamment petite pour que la vitesse du fluide soit la même en tous ses points (répartition uniforme).
2.2 - Conservation du débit
Considérons un tube de courant entre deux sections S1 et S1. Pendant l'intervalle de temps Dt, infiniment petit, la masse Dm1 de fluide ayant traversé la section S1 est la même que la masse Dm2 ayant traversé la section S2.
![]() En régime stationnaire, le
débit-masse est le même à travers toutes les sections droites
d'un même tube de courant.
En régime stationnaire, le
débit-masse est le même à travers toutes les sections droites
d'un même tube de courant.
Dans le cas d'un écoulement isovolume ( = Cte) :
![]() En régime
stationnaire, le débit-volume est le même à travers toutes les sections droites
d'un même tube de courant
En régime
stationnaire, le débit-volume est le même à travers toutes les sections droites
d'un même tube de courant
2.3 - Expression du débit en fonction de la vitesse v
Le débit-volume est aussi la quantité de liquide occupant un volume cylindrique de base S et de longueur égale à v, correspondant à la longueur du trajet effectué pendant l'unité de temps, par une particule de fluide traversant S.
Il
en résulte la relation importante :
![]()
2.4 - Vitesse moyenne
 |
Dans une section droite S de la canalisation, on appelle vitesse
moyenne vm la
vitesse telle que : 
La vitesse moyenne vmoy apparaît comme la vitesse uniforme à travers la section S qui assurerait le même débit que la répartition réelle des vitesses.
Si l'écoulement est isovolume, cette vitesse moyenne est inversement proportionnelle à l'aire de la section droite.
![]() C'est l'équation de continuité.
C'est l'équation de continuité.
![]() La vitesse moyenne est d'autant plus grande que la section est faible.
La vitesse moyenne est d'autant plus grande que la section est faible.
3 - Théorème de BERNOULLI
3.1 - Le phénomène
Observations
· Une balle de ping-pong peut rester en suspension dans un jet d'air incliné.
· Une feuille de papier est aspirée lorsqu'on souffle dessus.
Conclusion : La pression d'un fluide diminue lorsque sa vitesse augmente.
3.2 - Théorème de Bernoulli pour un écoulement permanent d’un fluide parfait incompressible
Un fluide parfait est un fluide dont l'écoulement se fait sans frottement.
 On considère un
écoulement permanent isovolume d’un fluide parfait, entre les sections S1
et S2, entre lesquelles il n’y a aucune machine hydraulique, (pas de
pompe, ni de turbine).
On considère un
écoulement permanent isovolume d’un fluide parfait, entre les sections S1
et S2, entre lesquelles il n’y a aucune machine hydraulique, (pas de
pompe, ni de turbine).
Soit m la masse et V le volume du fluide qui passe à travers la section S1 entre les instants t et t+Dt. Pendant ce temps la même masse et le même volume de fluide passe à travers la section S2. Tout se passe comme si ce fluide était passé de la position (1) à la position (2).
En appliquant le théorème de l’énergie cinétique à ce fluide entre les instants t et t+Dt (la variation d’énergie cinétique est égale à la somme des travaux des forces extérieures : poids et forces pressantes), on obtient :

p est la pression
statique,
![]() est la pression de
pesanteur,
est la pression de
pesanteur,
![]() est la pression cinétique.
est la pression cinétique.
Tous les termes s’expriment en pascal.
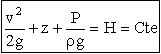 En
divisant tous les termes de la relation précédente par le produit g, on écrit tous les termes dans la dimension d'une hauteur (pressions exprimées en mètres
de colonne de fluide).
En
divisant tous les termes de la relation précédente par le produit g, on écrit tous les termes dans la dimension d'une hauteur (pressions exprimées en mètres
de colonne de fluide).
H est la Hauteur totale,
![]() est la Hauteur
de Pression, z est la cote,
est la Hauteur
de Pression, z est la cote,
![]() est la Hauteur cinétique,
est la Hauteur cinétique,
![]() est la Hauteur
piézomètrique.
est la Hauteur
piézomètrique.
3.3 - Cas d'un écoulement (1)®(2) sans échange de travail
Lorsque, dans un écoulement d’un fluide parfait, il n'y a aucune machine (ni pompe ni turbine) entre les points (1) et (2) d'une même ligne de courant, la relation de Bernoulli peut s’écrire sous l'une ou l'autre des formes suivantes :
![]() ou
ou ![]()
3.4 - Cas d'un écoulement (1)®(2) avec échange d’énergie
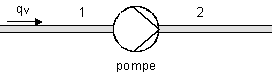 Lorsque le fluide
traverse une machine hydraulique, il échange de l’énergie avec cette machine
sous forme de travail DW pendant une
durée Dt. La puissance P échangée est
Lorsque le fluide
traverse une machine hydraulique, il échange de l’énergie avec cette machine
sous forme de travail DW pendant une
durée Dt. La puissance P échangée est
![]()
Unités : P en watt (W), W en joule (J), t en seconde (s).
· P > 0 si l’énergie est reçue par le fluide (ex. : pompe) ;
· P< 0 si l’énergie est fournie par le fluide (ex. : turbine).
Si le débit-volume est qv,
la relation de Bernoulli s’écrit alors :
![]()
4 - Application du Théorème de Bernoulli :
4.1 - 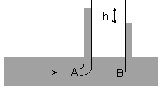 Tube de pitot
Tube de pitot
On considère un liquide en écoulement permanent dans une canalisation et deux tubes plongeant dans le liquide, l'un débouchant en A face au courant, et l'autre en B est le long des lignes de courant, les deux extrémités étant à la même hauteur. Au point B, le liquide a la même vitesse v que dans la canalisation et la pression est la même que celle du liquide pB = p.
En A, point d'arrêt, la vitesse est nulle et la pression est pA.
D'après le théorème de Bernoulli,
![]()
![]()
En mesurant la dénivellation h du liquide dans les deux tubes, on peut en déduire la vitesse v d'écoulement du fluide.
4.2 - Phénomène de Venturi
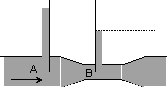 Un conduit de
section principale SA subit un étranglement en B où sa section est SB.
La vitesse d’un fluide augmente dans l’étranglement, donc sa pression y
diminue : vB > vA Þ pB < pA
Un conduit de
section principale SA subit un étranglement en B où sa section est SB.
La vitesse d’un fluide augmente dans l’étranglement, donc sa pression y
diminue : vB > vA Þ pB < pA
Le théorème de Bernoulli s'écrit ici :
![]()
D'après l'équation de
continuité,
![]() et
et
![]() donc
donc
![]()
![]() La différence de pression aux
bornes aux extrémités du tube de Venturi est proportionnelle au carré du
débit ; application à la mesure des débits (organes déprimogènes).
La différence de pression aux
bornes aux extrémités du tube de Venturi est proportionnelle au carré du
débit ; application à la mesure des débits (organes déprimogènes).
On peut citer aussi la trompe à eau, le pulvérisateur...
4.3 - Écoulement d'un liquide contenu dans un réservoir - Théorème de Torricelli
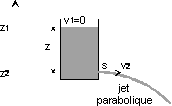 Considérons un
réservoir muni d'un petit orifice à sa base, de section s et une ligne de
courant partant de la surface au point (1) et arrivant à l'orifice au point
(2). En appliquant le théorème de Bernoulli entre les points (1) et (2),
Considérons un
réservoir muni d'un petit orifice à sa base, de section s et une ligne de
courant partant de la surface au point (1) et arrivant à l'orifice au point
(2). En appliquant le théorème de Bernoulli entre les points (1) et (2),
![]()
Or p1 = p2 = pression
atmosphérique ett v1<<v2 d'où
![]()
La vitesse d'écoulement est la même que la vitesse de chute libre entre la surface libre et l'orifice, quelle que soit la masse volumique du liquide.
Application : vase de Mariotte à débit constant.
VISCOSITE (F2)
1 - Le phénomène
1.1 - Observations
· L'eau, l'huile, le miel coulent différemment : l'eau coule vite, mais avec des tourbillons ; le miel coule lentement, mais de façon bien régulière.
· La chute d'un parachutiste se fait à vitesse constante, contrairement à la loi de la chute libre.
· La pression d'un liquide réel diminue tout au long d'une canalisation dans laquelle il s'écoule, même si elle est horizontale et de section uniforme, contrairement au théorème de Bernoulli.
1.2 - Conclusion
· Dans un fluide réel, les forces de contact ne sont pas perpendiculaires aux éléments de surface sur lesquelles elles s'exercent. La viscosité est due à ces frottements qui s'opposent au glissement des couches fluides les unes sur les autres.
· Les phénomènes dus à la viscosité des fluides ne se produisent que lorsque ces fluides sont en mouvement.
2 - Viscosité dynamique - Viscosité cinématique
2.1 - Profil des vitesses
Sous l'effet des forces d'interaction entre les molécules de fluide et des forces d'interaction entre les molécules de fluide et celles de la paroi, chaque molécule de fluide ne s'écoule pas à la même vitesse. On dit qu'il existe un profil de vitesse.
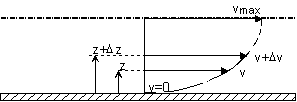 |
Le mouvement du fluide peut être considéré comme résultant du glissement des couches de fluide les unes sur les autres.
La vitesse de chaque couche est une fonction de la distance z de cette courbe au plan fixe : v = v(z).
2.2 - Viscosité dynamique
Considérons deux couches de fluide contiguës distantes de Dz. La force de frottement F qui s'exerce à la surface de séparation de ces deux couches s'oppose au glissement d'une couche sur l'autre. Elle est proportionnelle à la différence de vitesse des couches soit Dv, à leur surface S et inversement proportionnelle à Dz :
|
|
Le facteur de proportionnalité est le coefficient de viscosité dynamique du fluide.
Dimension : [] = M·L-1·T-1.
Unité : Dans le système international (SI), l'unité de viscosité dynamique est le Pascal seconde (Pa×s) ou Poiseuille (Pl) : 1 Pa·s = 1 Pl = 1 kg/m·s
Autres unités (non légales) :
On trouve encore les tables de valeurs numériques le coefficient de viscosité dans un ancien système d'unités (CGS) : l'unité est le Poise (Po) ; 1 Pl = 10 Po = 1 daPo = 103 cPo.
La viscosité de produits industriels (huiles en particulier) est exprimée au moyen d'unités empiriques : degré ENGLER en Europe, degré Redwood en Angleterre, degré Saybolt aux USA.
2.3 - Viscosité cinématique
Dans de nombreuses formules apparaît le rapport de la viscosité dynamique et de la masse volumique .
Ce rapport est appelé viscosité cinématique :
![]() Dimension
: [] = L2·T-1.
Dimension
: [] = L2·T-1.
Unité : Dans le système international (SI), l'unité de viscosité n'a pas de nom particulier : (m2/s).
Dans le système CGS (non légal), l'unité est le Stokes (St) : 1 m2/s = 104 St
2.4 - Ordre de grandeur ; influence de la température
|
Fluide |
h (Pa·s) |
|
eau (0 °C) |
1,787 x 10–3 |
|
eau (20 °C) |
1,002·x 10–3 |
|
eau (100 °C) |
0,2818·x 10–3 |
|
huile d'olive (20 °C) |
» 100·x 10–3 |
|
glycérol (20 °C) |
» 1,0 |
|
H2 (20 °C) |
0,860·x 10–5 |
|
O2(20 °C) |
1,95·x 10–5 |
La viscosité des liquides diminue beaucoup lorsque la température augmente.
Il n'existe pas de relation rigoureuse liant et T.
Contrairement à celle des liquides, la viscosité des gaz augmente avec la température.
3 - Mesurage de viscosités
3.1 - Viscosimètre d'Ostwald (voir T.P.)
On mesure la durée d'écoulement t d'un volume V de liquide à travers un tube capillaire. On montre que la viscosité cinématique n est proportionnelle à la durée t. Si on connaît la constante de l'appareil (K) fournie par le constructeur : n = K·t
Si on ne connaît pas cette constante, on la détermine préalablement à l'aide de l'eau.
3.2 - Viscosimètre à chute de bille ou viscosimètre d'Hoepler
 Une bille sphérique tombe
lentement dans un tube bien calibré renfermant le liquide visqueux. On mesure
la durée t que met la bille pour parcourir une certaine distance. On
montre que la viscosité dynamique h est proportionnelle à la durée t : h = K·t
Une bille sphérique tombe
lentement dans un tube bien calibré renfermant le liquide visqueux. On mesure
la durée t que met la bille pour parcourir une certaine distance. On
montre que la viscosité dynamique h est proportionnelle à la durée t : h = K·t
3.3 - Viscosimètre rotatif ou viscosimètre de Couette
|
|
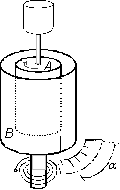
Un cylindre plein (A) tourne à vitesse constante dans un liquide contenu dans un récipient cylindrique (B) ; celui-ci, mobile autour de son axe de révolution, est entraîné par le liquide. Un ressort, exerçant un couple de torsion après avoir tourné d'un angle a, retient (B) en équilibre.
On montre que la viscosité dynamique h est proportionnelle à l'angle a : h = K·a
3.4 - Applications ; conséquences
La propulsion par hélice d’un avion ou d’un bateau est possible grâce à la viscosité de l’air ou de l’eau.
A cause de sa viscosité, la pression d’un fluide réel diminue en s’écoulant dans une canalisation ; cela nécessite parfois d’introduire des pompes à distance régulière tout au long de la canalisation.
PERTES DE CHARGE (F3)
1 - Le phénomène
Observations
· La pression d'un liquide réel diminue tout au long d'une canalisation dans laquelle il s'écoule, même si elle est horizontale et de section uniforme, contrairement au théorème de Bernoulli.
· La pression d'un fluide réel diminue après le passage à travers un coude, une vanne ou un rétrécissement.
Conclusion
· Un fluide réel, en mouvement, subit des pertes d'énergie dues aux frottements sur les parois de la canalisation (pertes de charge systématiques) ou sur les "accidents" de parcours (pertes de charge singulières).
2 - Les différents régimes d'écoulement : nombre de Reynolds
 |
En utilisant des fluides divers (viscosité différente), en faisant varier le débit et le diamètre de la canalisation, Reynolds a montré que le paramètre qui permettait de déterminer si l'écoulement est laminaire ou turbulent est un nombre sans dimension appelé nombre de Reynolds et donné par :
 ou
ou  avec :
avec :
r= masse volumique du fluide, v = vitesse moyenne, D = diamètre de la conduite
h= viscosité dynamique du fluide, n = viscosité cinématique
![]()
L'expérience montre que :
si Re < 2000 le régime est LAMINAIRE
si 2000 < Re< 3000 le régime est intermédiaire
si Re > 3000 le régime est TURBULENT
Ces valeurs doivent être considérées comme des ordres de grandeur, le passage d'un type d'écoulement à un autre se faisant progressivement.
3 - Théorème de Bernoulli appliqué à un fluide réel avec pertes de charge
Lors d'un écoulement d'un fluide réel il peut y avoir des pertes de charge entre les points (1) et (2) : dans le cas d’une installation ne comportant pas de machine hydraulique (pompe ou turbine) on écrira la relation de Bernoulli sous la forme :
![]()
· Dp représente l’ensemble des pertes de charge entre (1) et (2) exprimées en Pa.
4 - Expression des pertes de charge
4.1 - Influence des différentes grandeurs
Lorsqu'on considère un fluide réel, les pertes d'énergie spécifiques ou bien comme on les appelle souvent, les pertes de charge dépendent de la forme, des dimensions et de la rugosité de la canalisation, de la vitesse d'écoulement et de la viscosité du liquide mais non de la valeur absolue de la pression qui règne dans le liquide.
La différence de pression p = p1 - p2 entre deux points (1) et (2) d'un circuit hydraulique a pour origine :
· Les frottements du fluide sur la paroi interne de la tuyauterie ; on les appelle pertes de charge régulières ou systématiques.
· La résistance à l'écoulement provoquée par les accidents de parcours (coudes, élargissements ou rétrécissement de la section, organes de réglage, etc.) ; ce sont les pertes de charge accidentelles ou singulières.
Le problème du calcul de ces pertes de charge met en présence les principales grandeurs suivantes :
Le fluide caractérisé par : · sa masse volumique r.
· sa viscosité cinématique n.
Un tuyau caractérisée par : · sa section (forme et dimension) en général circulaire (diamètre D), sa longueur L.
· sa rugosité k (hauteur moyenne des aspérités de la paroi).
Ces éléments sont liés par des grandeurs comme la vitesse moyenne d'écoulement v ou le débit q et le nombre de Reynolds Re qui joue un rôle primordial dans le calcul des pertes de charge.
4.2 - Pertes de charge systématiques
4.2.1 - Généralités
Ce genre de perte est causé par le frottement intérieur qui se produit dans les liquides ; il se rencontre dans les tuyaux lisses aussi bien que dans les tuyaux rugueux.
Entre deux points séparés par une longueur L, dans un tuyau de diamètre D apparaît une perte de pression p. exprimée sous la forme suivante :


Différence de pression (Pa) Perte de charge exprimée en mètres de colonne de fluide (mCF)
est un coefficient sans dimension appelé coefficient de perte de charge linéaire.
Le calcul des pertes de charge repose entièrement sur la détermination de ce coefficient l.
4.2.2 - Cas de l'écoulement laminaire : Re < 2000
Dans ce cas on peut montrer que le coefficient est uniquement fonction du nombre de Reynolds Re ; l'état de la surface n'intervient pas et donc ne dépend pas de k (hauteur moyenne des aspérités du tuyau), ni de la nature de la tuyauterie.
![]() avec
avec ![]()
Il est alors immédiat de voir que h est proportionnel à la vitesse v et donc au débit q, ainsi qu'à la viscosité cinématique .
4.2.3 - 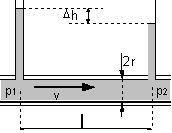 Loi de Poiseuille
Loi de Poiseuille
Pour un écoulement laminaire, dans une conduite cylindrique horizontale, le débit-volume d'un fluide est donné par :
|
|
avec :
· qv : débit-volume (m3·s–1),
· r : rayon intérieur (m),
· h : viscosité dynamique du fluide (Pa·s),
·
![]() : longueur entre les points (1) et (2) (m),
: longueur entre les points (1) et (2) (m),
· p1 et p2 : pression du fluide aux points (1) et (2) (Pa).
4.2.4 - Cas de l'écoulement turbulent : Re > 3000
Les phénomènes d'écoulement sont beaucoup plus complexes et la détermination du coefficient de perte de charge résulte de mesures expérimentales. C'est ce qui explique la diversité des formules anciennes qui ont été proposées pour sa détermination.
En régime turbulent l'état de la surface devient sensible et son influence est d'autant plus grande que le nombre de Reynolds Re est grand. Tous les travaux ont montré l'influence de la rugosité et on s'est attaché par la suite à chercher la variation du coefficient en fonction du nombre de Reynolds Re et de la rugosité k du tuyau.
La formule de Colebrook est actuellement considérée comme celle qui traduit le mieux les phénomènes d'écoulement en régime turbulent. Elle est présentée sous la forme suivante :

L'utilisation directe de cette formule demanderait, du fait de sa forme implicite, un calcul par approximations successives ; on emploie aussi en pratique des représentations graphiques (abaques).
Pour simplifier la relation précédente, on peut chercher à savoir si l'écoulement est hydrauliquement lisse ou rugueux pour évaluer la prédominance des deux termes entre parenthèses dans la relation de Colebrook.
Remarque :
On fait souvent appel à des formules empiriques plus simples valables pour des cas particuliers et dans un certain domaine du nombre de Reynolds, par exemple :
Formule de Blasius : (pour des tuyaux lisses et Re < 105)
![]()
4.3 - Pertes de charge accidentelles
Ainsi que les expériences le montrent, dans beaucoup de cas, les pertes de charge sont à peu près proportionnelles au carré de la vitesse et donc on a adopté la forme suivante d'expression :


Perte de charge exprimée en de pression (Pa). Perte de charge exprimée en mètres de colonne de fluide (mCF)
K est appelé coefficient de perte de charge singulière (sans dimension).
La détermination de ce coefficient est principalement du domaine de l'expérience.
5 - Théorème de Bernoulli généralisé
Lors d'un écoulement d'un fluide réel entre les points (1) et (2) il peut y avoir des échanges d'énergie entre ce fluide et le milieu extérieur :
· par travail à travers une machine, pompe ou turbine ; la puissance échangée étant P (voir Théorème de Bernoulli § 3.7)
· par pertes de charge dues aux frottements du fluide sur les parois ou les accidents de parcours ; la différence de pression étant Dp (voir ci-dessus § 3.1 et §3.2)
Le théorème de Bernoulli s'écrit alors sous la forme générale :
![]()
avec :
· SP : somme des puissances échangées entre le fluide et le milieu extérieur, à travers une machine, entre (1) et (2) :
P >0 si le fluide reçoit de l'énergie de la machine (pompe),
P <0 si le fluide fournit de l'énergie à la machine (turbine),
P = 0 s'il n'y a pas de machine entre (1) et (2).
· Dp : somme des pertes de charge entre (1) et (2) :
TENSION SUPERFICIELLE (F4)
1 - Le phénomène
Observations
· La surface libre de l'eau dans un tube forme un ménisque près des bords.
· Les poils d'un pinceau sec se rassemblent lorsqu'ils sont mouillés.
· Une aiguille fine en acier flotte à la surface de l'eau.
· L'eau monte dans un capillaire alors que le mercure descend.
· Une plaque de verre adhère très fortement à une surface plane lorsque celle-ci est mouillée.
· Une lame de savon prend une forme telle que sa surface soit minimale.
Conclusion
· La surface libre d’un liquide tend à se contracter spontanément de façon à acquérir une aire minimale.
· La surface d’un liquide se comporte un peu comme la membrane tendue d’un ballon.
2 - La force de tension superficielle
2.1 - Force de tension superficielle appliquée à un solide tiré par une lame liquide

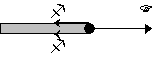 Considérons
un cadre ABCD dont le coté AB, de longueur L, peut glisser sur DA et CB. Plongé
initialement dans un liquide (par exemple de l'eau de savon), ce cadre est
rempli d'une lame mince liquide. Le liquide tire AB vers DC par une force f sur
chaque face de la lame, proportionnelle à la longueur L, telle que
Considérons
un cadre ABCD dont le coté AB, de longueur L, peut glisser sur DA et CB. Plongé
initialement dans un liquide (par exemple de l'eau de savon), ce cadre est
rempli d'une lame mince liquide. Le liquide tire AB vers DC par une force f sur
chaque face de la lame, proportionnelle à la longueur L, telle que ![]() .
.
Pour maintenir AB en
équilibre, il faut lui appliquer une force F (qui ne dépend pas de la
position de AB) telle que F = 2·f ou
![]()
avec F en N , L en m et g en N·m–1.
2.2 - Définition
Dans la relation précédente, le coefficient g s'appelletension superficielle du liquide.
Dimension : [g] = M. T-2.
Unité : Dans le système international (SI), l'unité de tension superficielle n'a pas de nom particulier : (N·m–1).
2.3 - Ordres de grandeur (dans le cas d'interface liquide-air)
|
liquide |
g (N·m–1) à 20 °C |
|
eau (à 20 °C |
73·x 10–3 |
|
eau (à 0 °C) |
75,6 x 10-3 |
|
huile végétale |
32·x 10–3 |
|
éthanol |
22·x 10–3 |
|
éther |
17·x 10–3 |
|
mercure |
480·x 10–3 |
2.4 - Angle qde raccordement liquide/solide
 Une goutte de liquide déposée sur une plaque solide plane et horizontale peut :
Une goutte de liquide déposée sur une plaque solide plane et horizontale peut :
· soit s'étaler largement (par exemple de l'eau sur du verre propre) ; dans ce cas, on dit que le liquide mouille parfaitement le solide, et l'angle de raccordement qvaut 0°,
· soit former une lentille :
· si q < 90°, le liquide mouille imparfaitement le solide (par exemple l'eau sur du verre sale)
· si q > 90°, le liquide ne mouille pas le solide (par exemple le mercure sur du verre).
Le même angle de raccordement se retrouve à la surface libre d'un liquide près des bords du récipient et provoque la formation d'un ménisque dans les tubes.
3 - Tube capillaire - loi de Jurin
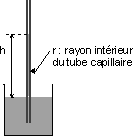 Un tube
capillaire (du latin capillus : cheveu) est un tube de petit diamètre intérieur.
Un tube
capillaire (du latin capillus : cheveu) est un tube de petit diamètre intérieur.
Lorsqu'on plonge un tube capillaire, ouvert aux deux extrémités, dans un liquide, celui-ci "monte" (si q < 90 °) ou "descend" (si q > 90 °) dans le tube d'une hauteur h telle que :
![]()
r : rayon intérieur du tube
r : masse volumique du liquide
g : intensité de la pesanteur
g : tension superficielle du liquide
q : angle de raccordement liquide/solide
4 - Mesurages de tension superficielle
4.1 - Méthode du capillaire
On applique la loi de Jurin. On mesure la dénivellation h et connaissant les autres paramètres, on en déduit une valeur de g.
4.2 - Méthode de la lame immergée ou de l'anneau immergé
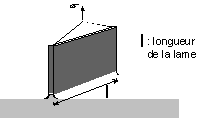 Une lame de
platine, parfaitement propre, de longueur L, plongée dans un liquide de
tension superficielle g, est
soutenue par le levier d'une balance de torsion qui permet de mesurer la force
F exercée sur la lame (le zéro est réglé lorsque la lame est dans l'air).
On soulève doucement la lame jusqu'à ce qu'elle affleure le liquide (la poussée
d'Archimède est alors nulle) et on mesure alors la force
Une lame de
platine, parfaitement propre, de longueur L, plongée dans un liquide de
tension superficielle g, est
soutenue par le levier d'une balance de torsion qui permet de mesurer la force
F exercée sur la lame (le zéro est réglé lorsque la lame est dans l'air).
On soulève doucement la lame jusqu'à ce qu'elle affleure le liquide (la poussée
d'Archimède est alors nulle) et on mesure alors la force
![]() . On en déduit une valeur de g.
. On en déduit une valeur de g.
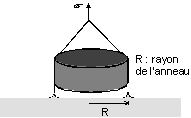 La lame peut être
remplacée par un anneau de rayon R, soutenu par un dynamomètre. On
soulève lentement l'anneau et, au moment de son arrachement de la
surface du liquide, on mesure la force
La lame peut être
remplacée par un anneau de rayon R, soutenu par un dynamomètre. On
soulève lentement l'anneau et, au moment de son arrachement de la
surface du liquide, on mesure la force
![]() . On en déduit une valeur de g.
. On en déduit une valeur de g.
4.3 - Méthode du stalagmomètre
Lorsqu'un liquide, de masse volumique r, s'écoule par un tube fin, le poids des gouttes obtenues est proportionnel à la tension superficielle g du liquide et au rayon extérieur R du tube : m·g = k·R·g
On compte le nombre N de gouttes qui s'écoulent pour un volume V donné délimité par deux traits de jauge gravés sur le tube. : N = V·r·g/(k·R·g)
Le stalagmomètre est étalonné avec de l'eau pure à 20 °C : N0 = V·r0·g/(k R·g0)
On obtient :
![]()
4.4 - Applications : agents tensioactifs
Le rôle des agents tensioactifs est d'abaisser la valeur de la tension superficielle des liquides dans lesquels ils sont ajoutés pour les rendre mouillants, moussants, détergents, émulsifiants...
Annexes
Bibliographie :
Mécanique 2 – AGATI (Dunod)
Mécanique expérimentale des fluides - COMOLET (Masson)
Mécanique des fluides – HANAUER (Breal)
Mesure des débits et vitesses des fluides – LEFEBVRE (Masson)
Mécanique des fluides (cours et exercices résolus) – MEIER (Masson)
Mécanique des fluides appliquée – OUZIAUX (Dunod Universités)
Mécanique / Phénomènes vibratoires – PRUNET (Dunod)
La Mécanique des fluides – SALIN (Natan Universités)
Avertissement :
Certaines parties de ce document dépassent le cadre du strict programme de terminale STL.
N'hésitez pas à contacter les auteurs pour leur communiquer vos remarques, questions, critiques constructives, compléments d'information :
Jacques CARBONNET Michel ROQUES mél : michel.roques@laposte.net