ETUDE DE LA TENSION SUPERFICIELLE D'UN LIQUIDE

ETUDE DE LA TENSION SUPERFICIELLE D'UN LIQUIDE

1 - Méthode de la lame :

1.1- Principe :

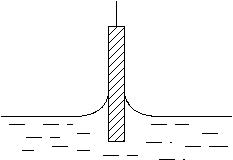
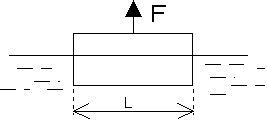
Une lame parfaitement propre d'épaisseur constante e, de longueur L (e « L) est plongée dans un liquide mouillant. Le liquide exerce sur elle une force d'attraction qui dépend de la nature du liquide et de la longueur de la lame.

Le module de la force est donné par : F = 2 g L

A est le coefficient de tension superficielle ; il varie avec la température et il dépend fortement des impuretés.
On utilisera une lame de platine de longueur 2 cm immergée dans différents liquides. La mesure de F se fera avec une balance de torsion, soit par arrachement, soit par la méthode de la lame immergée.

1.2- Manipulation et Résultats :

Le liquide à étudier est placé dans un cristallisoir parfaitement propre, posé sur un support à crémaillère. Avant chaque essai, nettoyer la lame de platine et la passer à la flamme soulever le cristallisoir pour amener le liquide en contact avec la lame ;celle-ci est attirée fortement ; descendre alors lentement le récipient et noter la plus grande valeur atteinte par l'index lumineux juste avant l'arrachement de la lame. L'intensité de la force est donnée en dynes; (1 dyne = 10^-5 N) ; faire plusieurs essais à la température ambiante.
En déduire la valeur du coefficient de tension superficielle g.

2- Loi de Jurin :

2.1- Principe :

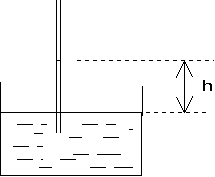
Lorsqu'un tube capillaire plonge dans un liquide, on observe une dénivellation dans le tube.
Cette dénivellation est donnée par la relation : h = 2 g / r r g .
r = rayon intérieur du tube
r = masse volumique du liquide
g est le coefficient de tension superficielle

2.2- Manipulation et Résultats :

A l'aide d'un cathétomètre viser le bas du ménisque (au préalable aspirer lentement celui-ci, puis le laisser prendre sa position d'équilibre), puis le niveau du liquide dans la cuve.
Pour chaque liquide, faire au moins trois essais concordants en remplissant un tableau de mesures et calculer la valeur moyenne de h.
En déduire la hauteur h.
Faire plusieurs essais en s'assurant de la propreté des tubes et de la cuve.
En déduire la valeur du coefficient de tension superficielle pour différents liquides (eau distillée, éthanol, méthanol, propan-1-ol, propan-2-ol).
Conclusion.

3- Méthode du dièdre

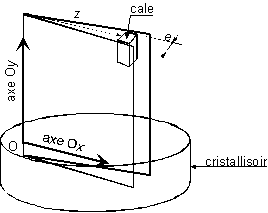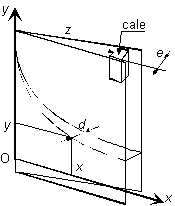
On remplace le tube capillaire par un dispositif formé de deux plaques en verre formant un dièdre selon le schéma ci-dessous. Les deux plaques sont maintenues par une pince large (type pince à dessin) sur l'arête du dièdre. La cale peut être un fil métallique calibré, ou un clou, de diamètre environ 1 mm.
On observe alors que la surface du liquide entre les deux plaques forme une courbe (hyperbole).
La dénivellation est inversement proportionnelle à la distance d entre les plaques.
On peut montrer que cette dénivellation est donnée par la relation :

3.1- Manipulation et résultats

Veiller à ne pas toucher les surfaces des plaques en verre avec les doigts.

Nettoyer soigneusement les deux plaques en verre et le cristallisoir, à l'aide d'acétone et de papier essuie-tout. Laisser sécher.
Mesurer l'épaisseur de la cale à l'aide d'un palmer : e =
Former un dièdre avec les deux plaques de verre à l'aide de la pince et de la cale.
Mesurer la distance entre la cale et l'arête du dièdre : z =
Poser le dièdre dans le cristallisoir (on peut le maintenir verticalement par une pince de chimie fixée sur un support).
Verser environ 100 mL d'eau distillée dans le cristallisoir en laissant couler l'eau entre les plaques.
Observer la surface libre du liquide entre les plaques et marquer quelques points de cette surface à l'aide du marqueur.
Mesurer la hauteur du liquide dans le cristallisoir à l'aide du réglet : H =
Sortir les plaques et les poser sur un papier essuie-tout.
Placer la plaque marquée sur une feuille de papier millimétré, le bord vertical sur l'axe des y et le bord inférieur parallèle à l'axe des x et à une ordonnée égale à - H de telle sorte que l'axe des x se trouve au niveau de la surface libre lors de l'expérience.
Mesurer l'abscisse x et l'ordonnée y des points marqués et remplir le tableau.

x (mm)
y (mm)

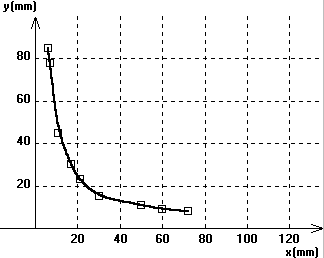
3.2- Interprétation
À l'aide du logiciel REGRESSI^® , entrer les mesures (en mètre), tracer le graphique y =f(x) et modéliser y = K/x
On admettra que l'eau et les liquides étudiés dans ce TP ont un angle de raccordement q égal à zéro.
Noter la valeur de K obtenue.
En déduire la tension superficielle du liquide g =
Imprimer (Tableau, Commentaire, Modélisation et Graphique).

Résultats :

Un tableur grapheur permet de modéliser la courbe expérimentale y = f(x)
et d'en déduire la valeur de la tension superficielle g .
Voici les résultats obtenus lors d'un premier essai
avec de l'eau déminéralisée (z = 90mm ; e = 2,5 mm) :

Le résultat de la modélisation par la relation
y(x)=2× g × z/(1000× 9,81× e× x) donne :

g = 0,0706 ±0,0024 N× m- ¹ (écart relatif 4,3%)

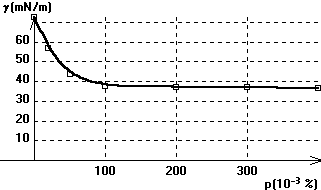
Étude d'une solution de détergent

La méthode précédente peut s'appliquer à l'étude de la variation de la tension superficielle d'une solution aqueuse de détergent en fonction de son pourcentage.
On peut partir d'une solution mère en diluant au 1/100 un "produit à vaisselle" commercial.
Cette solution servira à obtenir les solutions étudiées par dilutions suivantes.
Les résultats obtenus sont représentés sur le graphique ci dessous où p est le pourcentage volumique de détergent commercial.

On observe que la tension superficielle de la solution tend rapidement vers une limite
("quelques gouttes suffisent").

Page d'accueil retour TP mecafluides TP Physique