Simulation de chocs efficaces par ordinateur
 à l’aide du tableur EXCELâ  

1) Principe de la méthode

Ce document s’appuie sur le travail effectué par Guillaume BARBIER-CUEIL dont le fichier simulation_tirages.xls est disponible sur le site académique de Versailles. Il en explicite le fonctionnement.
On considère un réacteur fermé contenant les espèces A, B, C et D ainsi que le solvant S.
A et B sont susceptibles de réagir pour donner C et D et inversement selon : A + B = C + D 

La théorie des collisions prévoir que A et B (C et D) réagiront :

  1. S’il y a collision entre A et B (C et D)
  2. Si cette collision est efficace, c’est à dire si les 2 entités A et B (C et D) peuvent fournir une énergie au moins égale à l’énergie d’activation de la réaction.

Les collisions à envisager sont : (A,A) ; (B,B) ; (C,C) ; (D,D) ; (S,S) ; (A,B) ; (A,C) ; (A,D) ; (A,S) ; (B,C) ; (B,D) ; (B,S) ; (C,D) ; (C,S) et (D,S).

On se propose d’utiliser le tableur EXCEL pour simuler l’évolution des populations des espèces A, B, C et D en fonction du temps en étudiant l’évolution du nombre de boules A, B, C, D et S en fonction du nombre de tirages de 2 boules parmi l’ensemble des boules.
La probabilité Pii de tirages de 2 boules identiques (i et i) est donnée par la relation : 

La probabilité Pij de tirages de 2 boules i et j (i¹ j) est donnée par la relation :

 

avec nT = nA + nB + nC + nD +nS.

COMBIN(X ; Y) renvoie le nombre de combinaisons de Y éléments parmi les X éléments du système. Cette fonction ne fait pas la distinction entre le tirage (P,Q) et le tirage (Q,P).

La somme des probabilités des collisions entre deux entités appartenant au système est égale à 1 :
P(A,A) +P(B,B) +P(C,C)+P(D,D)+P(S,S)+P(A,B)+P(A,C)+P(A,D)+P(A,S)+P(B,C)+P(B,D)+P(B,S)+P(C,D) +P(C,S) +P(D,S) = 1.

Si on calcule les sommes des probabilités : 

P(A,A) ;
P(A,A) +P(B,B) ;
P(A,A) +P(B,B) +P(C,C) ;
P(A,A) +P(B,B) +P(C,C)+P(D,D) ;
P(A,A) +P(B,B) +P(C,C)+P(D,D)+P(S,S) ;
P(A,A) +P(B,B) +P(C,C)+P(D,D)+P(S,S)+P(A,B) ;
P(A,A) +P(B,B) +P(C,C)+P(D,D)+P(S,S)+P(A,B)+P(A,C) ;
P(A,A) +P(B,B) +P(C,C)+P(D,D)+P(S,S)+P(A,B)+P(A,C)+P(A,D) ;
P(A,A) +P(B,B) +P(C,C)+P(D,D)+P(S,S)+P(A,B)+P(A,C)+P(A,D)+P(A,S) ;
P(A,A) +P(B,B) +P(C,C)+P(D,D)+P(S,S)+P(A,B)+P(A,C)+P(A,D)+P(A,S)+P(B,C) ;
P(A,A) +P(B,B) +P(C,C)+P(D,D)+P(S,S)+P(A,B)+P(A,C)+P(A,D)+P(A,S)+P(B,C) +P(B,D) ;
P(A,A) +P(B,B) +P(C,C)+P(D,D)+P(S,S)+P(A,B)+P(A,C)+P(A,D)+P(A,S)+P(B,C) +P(B,D)+P(B,S) ;
P(A,A) +P(B,B) +P(C,C)+P(D,D)+P(S,S)+P(A,B)+P(A,C)+P(A,D)+P(A,S)+P(B,C) +P(B,D)+P(B,S)+P(C,D) ;
P(A,A) +P(B,B) +P(C,C)+P(D,D)+P(S,S)+P(A,B)+P(A,C)+P(A,D)+P(A,S)+P(B,C)+P(B,D)+P(B,S)+P(C,D)+P(C,S) ;
P(A,A) +P(B,B) +P(C,C)+P(D,D)+P(S,S)+P(A,B)+P(A,C)+P(A,D)+P(A,S)+P(B,C)+P(B,D)+P(B,S)+P(C,D)+P(C,S) . +P(D,S) ; 
on obtient une suite de nombres compris entre 0 et 1.

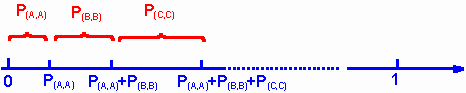
La fonction ALEA() d’EXCELâ   renvoie un nombre aléatoire compris entre 0 et 1. Il suffit alors de comparer la valeur de ALEA() aux valeurs des sommes calculées précédemment pour trouver le résultat du tirage aléatoire de 2 boules de l’urne.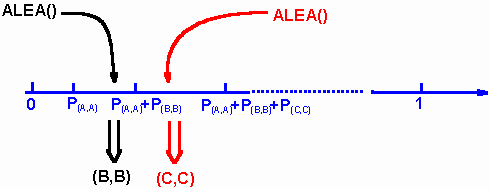

Exemple : 

Si ALEA() < P(A,A) le résultat du tirage est (A,A) ;
Si P(A,A) £ ALEA() < P(A,A) +P(B,B) le résultat du tirage est (B,B) ;
Si P(A,A) +P(B,B)  £ ALEA() < P(A,A) +P(B,B) +P(C,C) le résultat du tirage est (C,C) ;
Si P(A,A) +P(B,B) +P(C,C)+P(D,D)+P(S,S)+P(A,B) £ ALEA() < P(A,A) +P(B,B) +P(C,C)+P(D,D)+P(S,S)+P(A,B) + P(A,C)

le résultat du tirage est (A,C) ;

Pour les tirages (A,B) ou (C,D), il faut un critère pour décider si le choc est efficace. On utilise une nouvelle valeur de ALEA() à laquelle on compare le taux d’efficacité des chocs choisi par l’utilisateur. Si on considère par exemple que 70% des chocs sont efficaces, on considérera le choc comme efficace si ALEA() £ 0,70.
Des taux d’efficacité différents peuvent être choisis pour les chocs (A,B) et les chocs (C,D).

En fonction des résultats des tirages et de leur efficacité, trois cas sont à distinguer :

2) Quelques applications relatives à R + B = V + J (par analogie avec le tirage de boules Rouges, Bleues, Vertes et Jaunes).

2.1) Importance de l’efficacité des chocs (à relier à l’influence de la température).

Quantités initiales : 
50 boules rouges et 50 boules bleues
Efficacité directe : 80% ; Eff inverse : 0%

Quantités initiales : 
50 boules rouges et 50 boules bleues
Efficacité directe : 50% ; Eff inverse : 0%

2.2) Mise en évidence d’un état d’équilibre dynamique

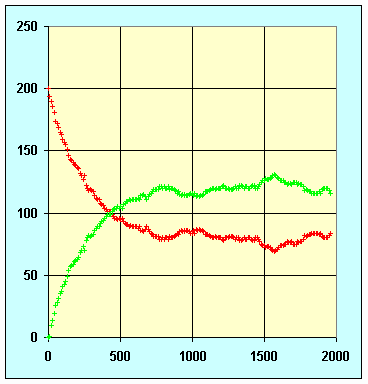
Quantités initiales : 200 boules rouges et 200 boules bleues 
Efficacité directe : 80% ; Eff inverse : 50%
A l ’équilibre, il y a plus de boules vertes et jaunes que bleues et rouges.

2.3) Le modèle a ses limites !

Quantités initiales 
 50 boules rouges et 50 boules bleues
Efficacités directe et inverse : 80%

Quantités initiales 
 200 boules rouges et 200 boules bleues 
Efficacités directe et inverse: 80%

L ’équilibre semble être plus " rapidement " atteint quand il y a moins d ’entités réactives !!!
On devrait obtenir les résultats suivants (résultats obtenus en résolvant l’équation différente par la méthode de Runge-Kutta (RK4) :

[R]0 = [B]0 = 0,1 mol/L 
kd = 0,2 ; ki = 0,1 L.mol-1.s-1

[R]0 = [B]0 = 0,5 mol/L 
kd = 0,2 ; ki = 0,1 L.mol-1.s-1

Hypothèse : On prend comme " incrément de temps " un tirage et on considère que pendant ce temps une seule rencontre a eu lieu ! alors que nT/2 rencontres ont eu lieu.

3) A propos de la feuille de calcul

Des précautions doivent être prises pour une bonne exécution de la feuille de calcul :

Lors du chargement du fichier tirages.xls, activer les macros.

    page d'accueil              Retour