RetourLa première loi de KEPLER |
||
 |
||
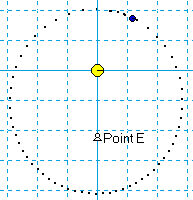
trajectoire, périodicité vitesse, accélération |
existence de foyers cas particulier de l'orbite circulaire |
|
Ouvrir le fichier KEPLER1A
Lancer la simulation et observer (planète sans vitesse initiale)
Décrire la trajectoire.
Observer le vecteur Accélération
Quelle force agit sur la
planète ? De quelles grandeurs dépend-elle ?
Expliquer pourquoi son mouvement
n'est pas uniformément accéléré.
Ouvrir le fichier KEPLER1B
Lancer la simulation et observer (planète avec vitesse initiale Vx = 3 m/s)
Décrire la trajectoire.
Comment varie le module |V|
de la vitesse de la planète ?
Ouvrir le fichier KEPLER1C
Lancer la simulation, observer le vecteur vitesse, puis afficher les vecteurs force et accélération.
Comment se comportent
l'accélération et la force au cours du mouvement ?
Faire apparaître le lecteur de bande : celui-ci apparaît en bas de l'écran (fenêtre en plein écran)
Déterminer la
période du mouvement.
Pour comparer les formes des ellipses, on définit leur excentricité
· Ouvrir le fichier KEPLER1D
Modifier les composantes initiales Vx et Vy de la planète à l'aide des curseurs
Pour pouvoir comparer différentes trajectoires : décocher l'option 'Autoeffacement de la trace' ( menu Monde)
· Ouvrir les fichiers
KEPLER1E et KEPLER1F dans 2 fenêtres (en tuile) : lancer la
simulation dans chaque fenêtre.
Recherche documentaire :
Rechercher la définition précise de l'excentricité. Faire un schéma.
Comparer les excentricités des orbites des différentes planètes du système solaire.
Haut
de page
Pour montrer que la trajectoire de la planète est effectivement une ellipse :
nous utiliserons une définition géométrique de l'ellipse, connue sous le nom d' ELLIPSE DU JARDINIER
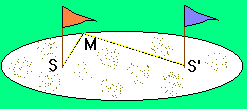
2 piquets sont plantés en S et S', les extrêmités d'une corde (inextensible) y sont fixées : il suffit de tendre la corde pour définir l'ensemble des points M appartenant à l'ellipse. On a la relation métrique :
MS + MS' = constante (1)
les points S et S' sont appelés foyers
Dans notre simulation :
La planète est au périhélie quand elle est la plus proche du Soleil, elle est à l'aphélie quand elle en est la plus éloignée.
On se propose de vérifier la relation (1), de déterminer le point équant et d'étudier le cas limite de l'orbite circulaire.
Ouvrir le fichier KEPLER1G
et lancer la simulation
Des compteurs permettent de visualiser l'évolution des distances D1 et D2 de la planète aux foyers, et leur somme D, et de repérer les positions x et y de la planète.
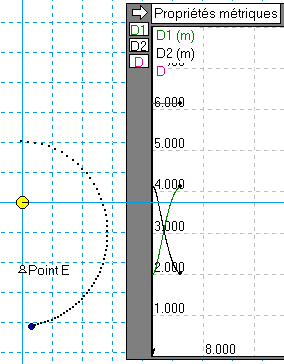
Déterminer les
coordonnées des points
P (périhélie),
A (aphélie) et
E (point équant).
Quelle est la direction du grand axe ?
Passer en mode Edition (menu Edition mode édition)
Modifier la composante Vy de la planète : Vy = 1 m/s
Utiliser de préférence le bouton :
pour modifier les propriétés de la planète Mass[3] |
 |
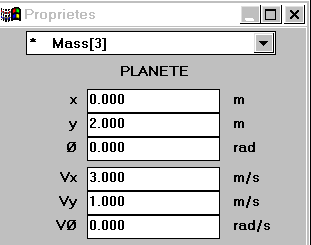Relancer la simulation.
Observer la nouvelle direction prise par le grand axe.
Déterminer la nouvelle
position du point équant :
 |
En s'aidant de considérations de symétrie, amener l'objet E le plus près possible de ce point, pour que la somme D reste constante au cours du mouvement. |  |
Vérifier la validité des résultats en utilisant la simulation.
Ouvrir le fichier KEPLER1H
les conditions initiales pour la planète sont les suivantes : x = 0 ; y = 2 et Vy = 0
On cherche à modifier la vitesse initiale de la planète pour obtenir une trajectoire circulaire :
Que peut-on dire du point E
dans ce cas ?
On agira uniquement sur la composante Vx de la vitesse en utilisant le contrôle :
 |
Essayer d'abord 4 m/s puis 2 m/s ... |  |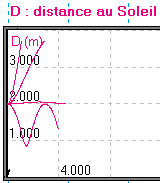
Noter la valeur de Vx
correspondant au mouvement circulaire
Ouvrir le fichier KEPLER1I
| Lancer la simulation |  |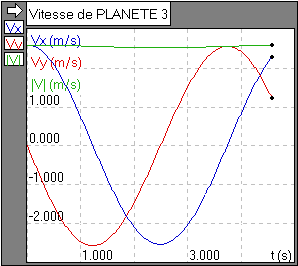
Noter la valeur de |V| |
Quelle est la nature du mouvement
de la planète ?
En appliquant la
relation fondamentale de la dynamique,
calculer précisément la valeur de |V|.
Affiner la valeur de la vitesse de la planète et vérifier par simulation.
Haut
de page
