 |
 |
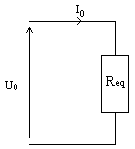 |
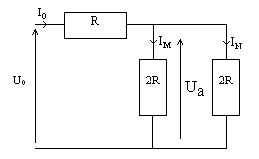
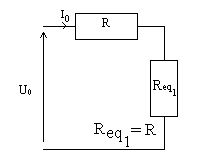
| * Schéma étudié : | * Schéma équivalent : |
CONVERTISSEUR |
I) Montage R-2R :
1) Etude théorique :
 |
 |
 |
| * Schéma étudié : | * Schéma équivalent : |
1.1) Donner l’expression littérale de la résistance équivalente Req en fonction de R, puis celle de l’intensité Io en fonction de Uo et Req (appliquer la loi d'Ohm) :
1.2) Exprimer Io en fonction IM et de IN :
1.3) Exprimer (en utilisant la loi d'Ohm) IM en fonction de Ua et 2.R, puis IN en fonction de Ua et 2.R.
En déduire la relation entre IM et IN
1.4) En utilisant les résultats du 1.2 et 1.3, trouver la relation entre Io et IM, puis exprimer IM en fonction de Io.
1.5 ) Exprimer IM en fonction de Uo et 4.R
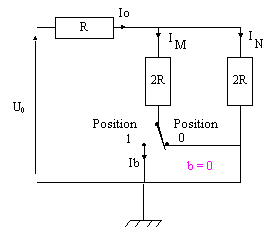
2) Etude d'un montage R-2.R associé à un interrupteur
On associe une variable logique b à un interrupteur.
- interrupteur en position 1 : b = 1
- interrupteur en position 0 : b = 0
 |
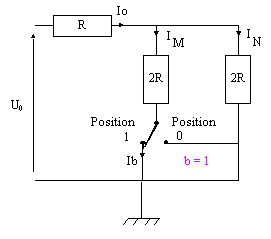 |
En observant les deux montages précédents, il est possible de donner l’expression du courant Ib suivant l’état de la variable logique b. Compléter :
* quand b = 0, alors Ib = .....................
|
II) Etude d’un convertisseur R-2R "2 bits" :
A chaque interrupteur est associé une variable logique, bo pour l'interrupteur de droite, b1 pour l'interrupteur de gauche (voir schéma ci-dessous)
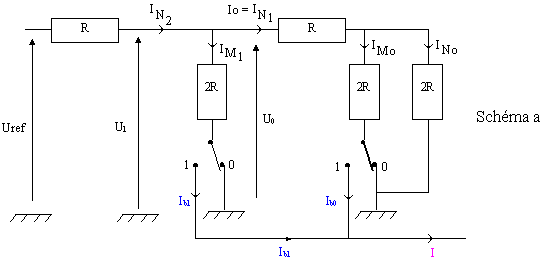
1) Quelle est la relation entre les tensions U1 et U0 ?
2) En reprenant les résultats précédents obtenus au I)2), exprimer Ibo en fonction de bo et IMo , puis Ib0 en fonction de bo, Uo et 4.R :
3) Exprimer Ibo en fonction de bo, U1 et 4.R.
4) Etude du cas où b0 = 0 et b1 = 0. Le montage étudié peut alors se réduire de la façon suivante :
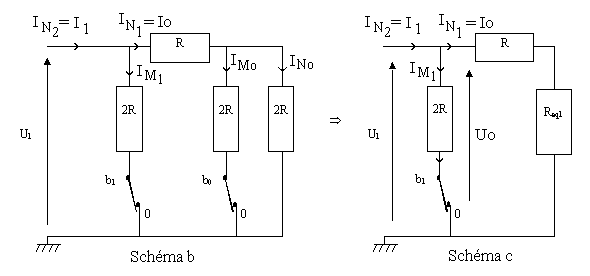
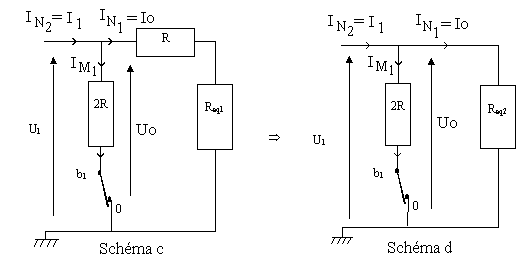
4.1) D'après les résultats du I) donner l’expression de Req1 en fonction de R, puis celle de Req2 en fonction de R :
4.2) D’après le schéma d et les résultats du paragraphe I)1), donner l’expression de IN1 en fonction de IM1 :
4.3) Donner la relation de I1 en fonction de IM1 et IN1 :
4.4) En appliquant la loi d'Ohm, donner l'espression de IM1 en fonction de U1 et 2.R :
5) En reprenant les notations du schéma a et les résultats du I) 2)
5.1) Exprimer Ib1 en fonction de b1 et IM1, puis en fonction de b1, U1 et 2.R : :
5.2) Exprimer I en fonction de Ib1 et Ib0 :
5.3) D'après l'expression de Ibo obtenue au II) 2) et les 2 relations trouvées précédemment, exprimer I en fonction de bo, b1, IM1 et IMo :
5.4) D'après les résultats précédent montrer que :
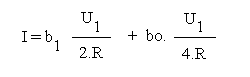
6) Etude du schéma équivalent final :
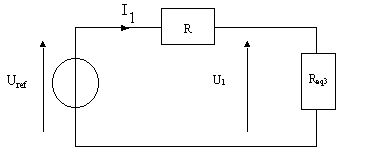 Req3 = R
Req3 = ROn montre que U1 = Uref /2
Réécrire l'expression de I en fonction de Uref, bo, b1 et 2.R
7) Codage d’un nombre N sur 2 bits b1 et b0 :
Si on code le nombre N, ce dernier sera égal à :
On montre que I peut s’écrire :
La relation précédente nous permet d’écrire que :
8) Etude de l’amplification finale :
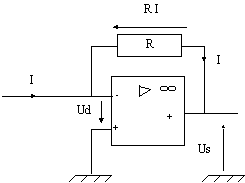 |
* En appliquant la loi des mailles, donner l’expression de Us en fonction de R I et Ud :
|
III) Etude expérimentale d’un Convertisseur Numérique-Analogique codé sur 4 bits :
1) Le montage final est le suivant :
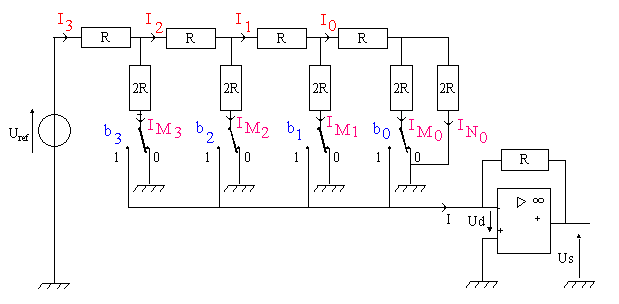
2) Relations utiles :
2.1) En s’inspirant des résultats obtenus au paragraphe II) 7), donner l’expression de I en fonction de Uref, R et N (le convertisseur à réseau R-2R est codé sur 4 bits).
2.2) Quelle est l’expression de Us en fonction de Uref et N?
3) Remplir le tableau en utilisant l’expression précédente de Us (Us théorique), sachant que Uref =5V, puis alimenter correctement la maquette et relever les valeurs expérimentales de Us.
3.1) Comparer les valeurs de Us théorique et Us expérimental.
3.2) Tracer la caractéristique de Us théorique en fonction du nombre N, Us expérimental en fonction du nombre N, puis conclure
| IV) Etude des convertisseurs CAN -CNA de l’interface ORPHY : |
1) Préparation du matériel :
* Relier l’interface "ORPHY" au port série de l’ordinateur (Mettre l’interface sous tension).
2) Etude du CAN :
* Relier le module TEST d'Orphy au connecteur A de l'interface.
2.1) Placer un générateur de tension entre les bornes 4 (EAO) et 3 (REF) du module TEST. Cette tension Ue sera réglable de 0 à 5V.
2.2) Lancer le logiciel CAN_CNA.
2.3) Faire un tableau de mesures qui indique les valeurs numériques de N obtenues à l’écran pour différentes valeurs de la tension Ue en entrée de l’interface ORPHY.
2.4) Tracer la caractéristique de transfert N en fonction de Ue. Conclure.
2.5) Donner un exemple de l’utilisation d’un Convertisseur Analogique-Numérique.
3) Etude du CNA :
* Relier le module TEST d'Orphy au connecteur C de l'interface.
3.1) Placer un voltmètre (à la place du générateur de tension) entre les bornes 1 (SA) et 2 (0V) du boîtier de raccordement. Ce voltmètre mesurera la tension Us en sortie de l’interface.
3.2) Lancer le logiciel CAN_CNA.
3.3) Faire un tableau de mesures qui indique les valeurs des tensions Us mesurées au voltmètre pour différentes valeurs numériques N entrées au clavier de l’ordinateur.
3.4) Tracer la caractéristique de transfert Us en fonction de N. Conclure.
I) Montage R-2R :
1) Etude théorique :
1.1) Donner l’expression littérale de la résistance équivalente Req en fonction de R, puis celle de l’intensité Io en fonction de Uo et Req (appliquer la loi d'Ohm) :
1.2) Exprimer Io en fonction IM et de IN :
1.3) Exprimer (en utilisant la loi d'Ohm) IM en fonction de Ua et 2.R, puis IN en fonction de Ua et 2.R.
En déduire la relation entre IM et IN
1.4) En utilisant les résultats du 1.2 et 1.3, trouver la relation entre Io et IM, puis exprimer IM en fonction de Io.
1.5 ) Exprimer IM en fonction de Uo et 4.R
2) Etude d'un montage R-2.R associé à un interrupteur
En observant les deux montages précédents, il est possible de donner l’expression du courant Ib suivant l’état de la variable logique b. Compléter :
* quand b = 0, alors Ib = ..................... * quand b = 1, alors Ib = ...................... * On peut dire que Ib = b x.. ?................. * Exprimer Ib en fonction de b et Io (utiliser le résultat du 1.4 ),
|
II) Etude d’un convertisseur R-2R "2 bits" :
1) Quelle est la relation entre les tensions U1 et U0 ?
2) En reprenant les résultats précédents obtenus au I)2), exprimer Ibo en fonction de bo et IMo
puis Ib0 en fonction de bo, Uo et 4.R :
3) Exprimer Ibo en fonction de bo, U1 et 4.R.
4) Etude du cas où bo = 0 et b1 = 0 :
4.1) D'après les résultats du I) donner l’expression de Req1 en fonction de R, puis celle de Req2 en fonction de R :
4.2) D’après le schéma d et les résultats du paragraphe I)1), donner l’expression de IN1 en fonction de IM1 :
4.3) Donner la relation de I1 en fonction de IM1 et IN1 :
4.4) En appliquant la loi d'Ohm, donner l'espression de IM1 en fonction de U1 et 2.R :
5) En reprenant les notations du schéma a et les résultats du I) 2) :
5.1) Exprimer Ib1 en fonction de b1 et IM1, puis en fonction de b1, U1 et 2.R : :
5.2) Exprimer I en fonction de Ib1 et Ib0 :
5.3) D'après l'expression de Ibo obtenue au II) 2) et les 2 relations trouvées précédemment, exprimer I en fonction de bo, b1, IM1 et IMo :
5.4) D'après les résultats précédent montrer que :
6) Etude du schéma équivalent final : U1 = Uref /2
Réécrire l'expression de I en fonction de Uref, bo, b1 et 2.R
7) Codage d’un nombre N sur 2 bits b1 et b0 :
Si on code le nombre N, ce dernier sera égal à :
On montrer que I peut s’écrire :
La relation précédente nous permet d’écrire que
8) Etude de l’amplification finale :
 |
* En appliquant la loi des mailles, * Comme Ud = 0, donner la nouvelle expression de Us : |
III) Etude expérimentale d’un Convertisseur Numérique-Analogique codé sur 4 bits :
2) Relations utiles :
2.1) En s’inspirant des résultats obtenus au paragraphe II) 7), donner l’expression de I en fonction de Uref, R et N (le convertisseur à réseau R-2R est codé sur 4 bits).
2.2) Quelle est l’expression de Us en fonction de Uref et N?
3) Remplir le tableau en utilisant l’expression précédente de Us (Us théorique), sachant que Uref =5V, puis alimenter correctement la maquette et relever les valeurs expérimentales de Us.
3.1) Comparer les valeurs de Us théorique et Us expérimental.
3.2) Tracer les caractéristiques de Us théorique en fonction du nombre N et de Us expérimental en fonction du nombre N, puis conclure.
IV) Etude des convertisseurs CAN -CNA de l’interface ORPHY :
2) Etude du CAN :
2.3) Faire un tableau de mesures qui indique les valeurs numériques de N obtenues à l’écran pour différentes valeurs de la tension Ue en entrée de l’interface ORPHY.
2.4) Tracer la caractéristique de transfert N en fonction de Ue. Conclure.
2.5) Donner un exemple de l’utilisation d’un Convertisseur Analogique-Numérique.
3) Etude du CNA :
3.3) Faire un tableau de mesures qui indique les valeurs des tensions Us mesurées au voltmètre pour différentes valeurs numériques N entrées au clavier de l’ordinateur.
3.4) Tracer la caractéristique de transfert Us en fonction de N. Conclure.