Chute amortie d’un bouchon
dans une "éprouvette géante"
Le projectile est un bouchon "style bouchon de pêche" voir le dispositif expérimental
D'après une idée de René Mélin
Caractéristiques de l'éprouvette : Tuyau de plexiglass
Hauteur : 2 mètres
Diamètre : 20 cm
Le tuyau est collé sur une plaque de plexi avec de la colle pour évacuation sanitaires .
Voir d'autres TP proposés
Enregistrements de vidéos avec une webcam Philips en formats 640x480 à 10
images par seconde.
(Téléchargements en fin de page)
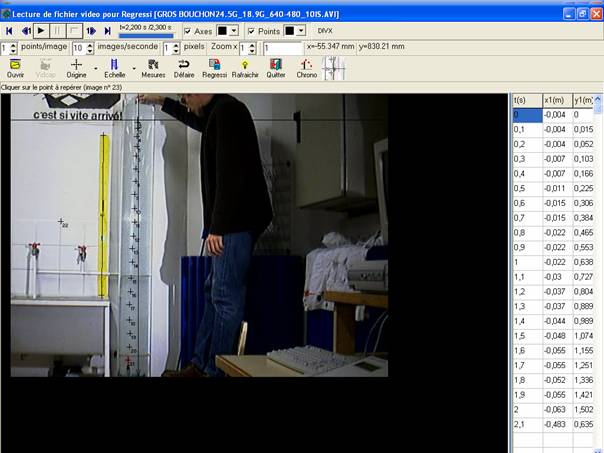
Masse du bouchon m = 24,5 g
Masse d’eau déplacée me = 18,8 g
Durée entre deux images 0,1 s
Nom du fichier : gros bouchon 24,5_18,9g_640-480_10is.avi
On reprend
le fichier dans le logiciel regavi, on numérise les points puis on traite les
données dans le logiciel regressi.
On dérive y par rapport au temps et on
obtient :
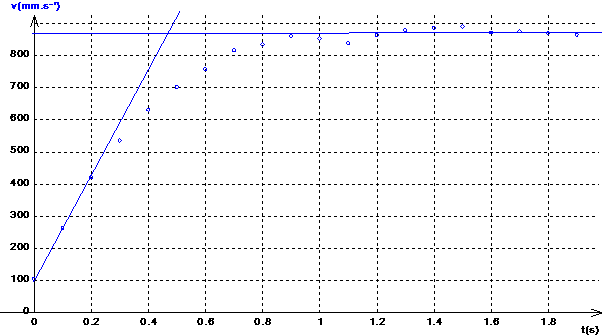
vitesse limite : vl = 0,87 m/s
vitesse
initiale : v0 = 0,1 m/s
I. Hypothèse d’une force en –k×v :
On applique
la seconde loi de Newton au système bouchon et on obtient :
Avec
(
poids) ;
(poussée d’Archimède) et
En
projetant sur un axe vertical vers le bas on obtient :
Quand v = vl
on a
et
On a
aussi :
Méthode
d’Euler :
ou
Résolution avec la calculette : Prendre une vitesse initiale v0 = 0.1 m/s et un pas Dt= 0,1 s
|
taper 0.1 |
EXE |
v0 = 0.10 |
|
taper Ans+ (2.24 –2.58xAns)x 0,1 |
EXE |
v1 = 0.298 |
|
|
EXE |
v2 = 0.445 |
|
EXE |
v3 = 0.554 |
|
|
etc ...... |
vn = 0.870 |
Chaque validation de la
touche EXE permet de calculer vn et donc la vitesse limite
On obtient les courbes
suivantes :
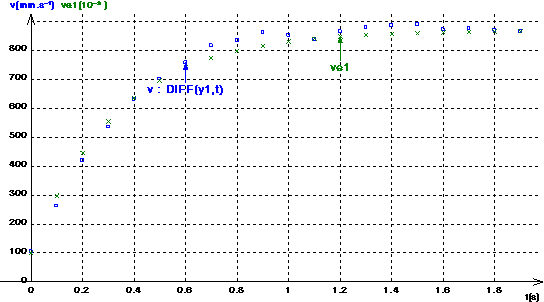
II. Hypothèse d’une force en –k×v2 :
On applique
la seconde loi de Newton au système bouchon et on obtient :
Avec
(
poids) ;
(poussée d’Archimède) et
En
projetant sur un axe vertical vers le bas on obtient :
Quand v = vl
on a
et
On a
aussi :
Méthode
d’Euler :
ou
Résolution avec la calculette : Prendre une vitesse initiale v0 = 0.1 m/s et un pas Dt= 0,1 s
|
taper 0.1 |
EXE |
v0 = 0.10 |
|
taper Ans+ (2.24 –2.96x(Ans)2)x 0,1 |
EXE |
v1 = 0.321 |
|
|
EXE |
v2 = 0.514 |
|
EXE |
v3 = 0.66 |
|
|
etc ...... |
vn = 0.870 |
Chaque validation de la
touche EXE permet de calculer vn et donc la vitesse limite
On obtient les courbes
suivantes :
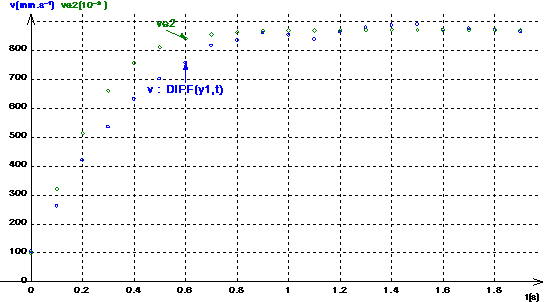
III.
Comparaison
des résultats :
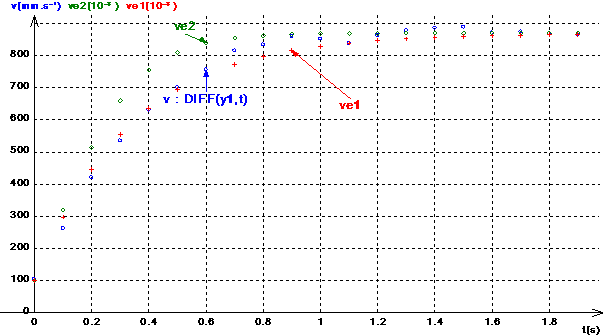
Le modèle en « -k×v » semble mieux convenir que celui en « -k×v2 »
Tableau des mesures :
i t x1 y1 ve1 ve2 v
s m m mm.s-1
0 0 -0,00369 0 0,1 0,1 104,4
1 0,1 -0,00369 0,01476 0,298 0,321 262,5
2 0,2 -0,00369 0,05166 0,445 0,514 420,6
3 0,3 -0,00738 0,1033 0,554 0,66 535
4 0,4 -0,00738 0,166 0,635 0,755 631
5 0,5 -0,01107 0,2251 0,695 0,81 701,1
6 0,6 -0,01476 0,3063 0,74 0,839 756,4
7 0,7 -0,01476 0,3837 0,773 0,855 815,4
8 0,8 -0,02214 0,4649 0,797 0,862 833,9
9 0,9 -0,02214 0,5535 0,816 0,866 859,7
10 1 -0,02214 0,6383 0,829 0,868 852,3
11 1,1 -0,02952 0,7269 0,839 0,869 837,6
12 1,2 -0,0369 0,8044 0,847 0,869 863,4
13 1,3 -0,0369 0,8892 0,852 0,87 878,2
14 1,4 -0,04428 0,9889 0,856 0,87 885,5
15 1,5 -0,04797 1,074 0,859 0,87 889,3
16 1,6 -0,05535 1,155 0,862 0,87 870,8
17 1,7 -0,05535 1,251 0,863 0,87 874,5
18 1,8 -0,05166 1,336 0,865 0,87 869,2
19 1,9 -0,05535 1,421 0,866 0,87 863,9
20
page d'accueil