Chute verticale d’un solide dans un liquide

1 Etude expérimentale :

- Enregistrement
Un objet (flotteur de pêche à la ligne lesté) est lâché sans vitesse initiale dans de l’eau. Un enregistrement vidéo est effectué avec une webcam à raison de 10 images par seconde.

- Saisie des positions d’un point en fonction du temps : Lancer le logiciel REGAVI. Charger le fichier intitulé « poisson2.avi » Vérifier le réglage du nombre d’images par seconde à la vitesse d’acquisition, soit 10 images/s. Indiquer l’échelle : la distance entre deux traits sur le support est de 50cm. Placer l’origine du repère sur la première position du mobile.Décocher l’option trace. Revenir au début de l’enregistrement. Lancer l’acquisition en cliquant sur la caméra et relever les positions successives du mobile. (24 positions) Transférer le résultat en Regressi (icône « stop » puis icône Regressi). Il peut être préférable d’ouvrir Regressi avant d’utiliser Regavi.

- Traitement des mesures.
Afficher la trajectoire : quel système de coordonnées faut-il choisir ?Le repère doit-il être orthonormé ? Quelle observation peut-on faire en ce qui concerne les valeurs de x ? Justifier. Est-il nécessaire de travailler dans un repère à deux dimensions pour l’étude du mouvement ?
Afficher y=f(t). L’option « axes orthonormés » a-t-elle un sens pour l’affichage de cette courbe ? Quel est le sens de l’axe y’y du repère ?
On souhaite travailler sur un axe Y’Y orienté vers le bas. Exprimer l’abscisse Y du mobile dans ce repère en fonction de y et ajouter la colonne correspondante dans le tableau.
Faire calculer la vitesse v à partir de Y (dérivée) et afficher v=f(t). Préciser les deux régimes du mouvement du solide.
Déterminer la vitesse limite acquise par le solide en modélisant la vitesse lors de la deuxième phase du mouvement par une constante (modèle prédéfini, manuelle, v = b). Quelle est la nature du mouvement du mobile dans cette phase ?
vl =__________________ nature du mouvement : _________________________________
Pourquoi la vitesse initiale n’est-elle pas nulle ? Relever sa valeur : v0 = _____________________

2 Equation différentielle du mouvement.

Système étudié, Référentiel choisi, Forces exercées sur le bouchon, schéma : 
Application de la deuxième loi de Newton : Etablissement de l’équation différentielle du mouvement.

Poussée d’Archimède : résumer la détermination de la masse d’eau déplacée (on place une éprouvette contenant de l’eau sur la balance et on tare, on introduit dans l’eau, le bouchon suspendu par un fil ; la masse indiquée par la balance correspond à la masse d’eau déplacée)   meau = ____________ ;  calculer, à partir de ce résultat, la valeur de la poussée d’Archimède s’exerçant sur le bouchon FA = _________________ Relever la masse du bouchon : msolide = ______________ et calculer son poids P =____________

Vitesse limite.
Au début du mouvement, la vitesse augmente, qu’en est-il de la force de frottement ? 
Que devient l’équation ci-dessus lorsque la vitesse atteint la valeur limite ?
En déduire la valeur de la constante k de la force de frottement et du rapport k/m.
Ecrire l’expression semi numérique définitive de l’équation différentielle :

3 – Résolution des équations différentielles par une méthode numérique itérative : la méthode d’Euler
3.1 Principe
La vitesse à la date i, vi peut être obtenue en ajoutant à la vitesse à la date i-1, vi-1 , la variation de vitesse Dvi-1 : vi = vi-1 + Dvi-1
Or l’accélération à la date i-1 , ai-1 , a pour valeur approchée le rapport si Dt est suffisamment petit ; on peut donc écrire : Dvi-1 = ai-1. Dt ; l’expression de vi devient : vi = vi-1 + ai-1. Dt
L’équation différentielle où intervient dv/dt c’est à dire a , permet de calculer ai-1 si vi-1 est connue. La répétition de ce raisonnement permet ensuite de calculer vi+1 puisque vi est alors connue, et ainsi de suite , d’où le nom de méthode numérique itérative (réitérer = recommencer)

3.2 Chute verticale dans un liquide.
traitement manuel : a partir de la vitesse v0 relevée précédemment, calculer v1 en appliquant la méthode d’Euler, l’intervalle de temps considéré étant l’intervalle entre deux images, soit 0,1s. recommencer le calcul pour v2 et comparer les résultats à ceux obtenus par le calcul en Regressi.
L’aspect fastidieux de ces calculs impose l’utilisation d’un tableur.

traitement par un tableur
transférer la tableau de Regressi vers Excel : enregistrer d’abord en fichier txt le tableau (et non avec l’extension RW3).
Lancer Excel et ouvrir le fichier précédent en demandant les fichiers txt.
Masquer les colonnes inutiles (format, colonne masquer). Limiter les chiffres significatifs (format, cellule, nombre) ; construire une nouvelle colonne appelée v euler ; la première valeur est la vitesse initiale ; 
Sélectionner la cellule suivante et y inscrire, après le signe = la relation numérique de calcul de la vitesse ; la vitesse qui intervient dans cette expression doit être précisée en cliquant dessus ou en donnant sa situation ( C6 par exemple). « tirer » la formule vers le bas pour remplir les cellules suivantes.
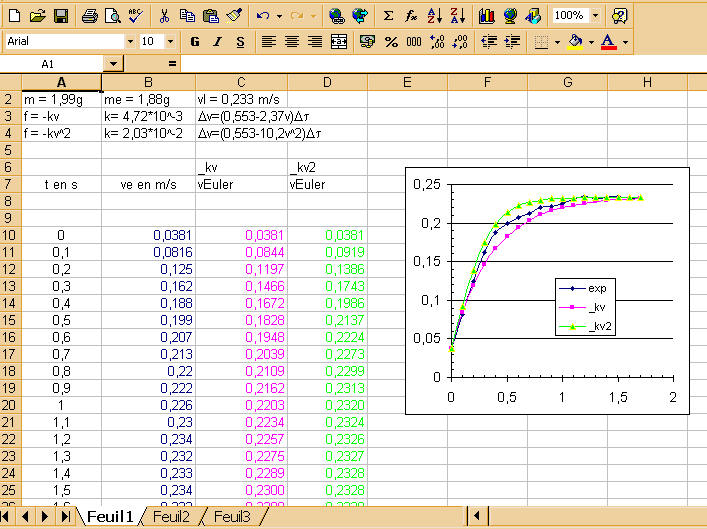
Afficher le graphique donnant la vitesse expérimentale et la vitesse obtenue par la méthode d’ Euler en fonction du temps

3.3 analyse de la force de frottement
L’hypothèse d’une force de frottement du type –kv2 ne colle pas tout à fait avec les relevés expérimentaux ; on peut donc rechercher un modèle différent et voir s’il s’approche mieux de l’expérience. On propose une force du type – kv.
Etablir dans ce cas l’équation différentielle ; déterminer de la même façon les valeurs numériques des constantes et utiliser le tableur pour comparer les différentes courbes v= f(t) ; conclure.

  Page d'accueil           Page terminale S           Vidéo et mécanique          Nouveaux programmes