La méthode d'Euler
Il s'agit certainement de la
méthode la plus simple d'intégration numérique.
Elle permet d'atteindre une prévision correcte des résultats expérimentaux si
le pas de résolution est « suffisamment » petit.
Elle permet une prévision de l'évolution, en fonction du temps, de la vitesse et
de la position d'un mobile.
On ne considèrera que des mouvements de translation
rectiligne.
Après un bilan des forces extérieures s'exerçant sur le mobile,
l'accélération est obtenue à partir de :
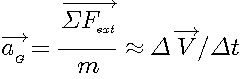
|
Il faut comprendre qu'entre deux
lignes consécutives,
|
Aussi est-il nécessaire de choisir des
incrémentations les plus petites possibles pour t, d'où un nombre de calculs
longs et fastidieux ...
L'utilisation d'un tableur s'impose.
|
EXEMPLES |
COMMENTAIRES |
|
Il permet de montrer
l'influence du pas sur les résultats obtenus |
|
|
Mouvement sinusoïdal amorti par des
frottements fluides du type : |
|
|
Mouvement de chute avec frottements |
Résolution numérique
d'une équation différentielle dont la solution analytique |
![]() Page d'accueil
Pages Physique Méthodes
numériques Nouveaux
programmes TS
Page d'accueil
Pages Physique Méthodes
numériques Nouveaux
programmes TS