 |
Présentation
Les documents qui suivent correspondent à une version
enrichie de ceux utilisés lors du stage " Mise en œuvre des méthodes
numériques avec un tableur " co-animé par Pierrette MAX et Maurice
SCHWING qui a eu lieu en mars 2002.
Ils se composent de cours (fichiers .pdf) incluant des
exercices (environ 50) dont les corrigés sont également disponibles (fichiers
.xls).
Ces documents ont été regroupés autour de quatre grands thèmes
 Résolution d'équations différentielles |
Méthode d’EULER (consulter
en ligne), Méthode de RUNGE-KUTTA d’ordre 2 et d’ordre 4 |
|
Dérivation numérique |
|
|
Intégration numérique |
|
|
Modélisation |
Régression
linéaire, Régression polynomiale, mise en œuvre du solveur d’EXCEL |
La lecture du chapitre relatif à la dérivation numérique nécessite la lecture préalable des chapitres relatifs aux régressions linéaires et polynomiales, les méthodes de dérivation numérique élaborées mettent en œuvre des lissages polynomiaux locaux.
| D’avance, nous remercions tous ceux
qui voudront bien nous faire part de leurs remarques ou de leurs
suggestions pour une amélioration des documents
proposés. Pour tout renseignement supplémentaire, vous pouvez vous adresser à : Maurice SCHWING IUFM de Lorraine, rue de la Victoire 57950 Montigny les Metz. |
Page d'accueil
Utilisation
d'un tableur
Résolution d'équations différentielles
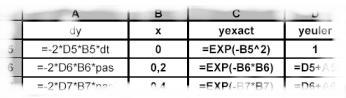
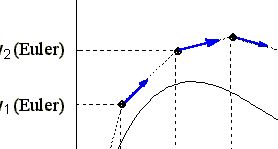
| La méthode
d'EULER (facile à appréhender) et les méthodes de RUNGE-KUTTA
d'ordre 2 (RK2) et 4 (RK4)
sont successivement introduites. Les exemples traités sont pris dans le programme des lycées. La présentation " géométrique " des méthodes RK2 et RK4 permet de bien comprendre le passage de yi à yi+1. |
|||
 Consulter
en ligne |
Cours (fichiers PDF)  |
Exercices (fichiers Excel ® ) | |
|
Méthode d'EULER
(220 ko) Méthode de RUNGE-KUTTA RK2 Méthode de RUNGE-KUTTA RK4 |
Exercices
1 à 9
(225 ko)
Exercices 1 et 2 Exercices 1
à 7 |
|
|
|
|||
|
|||
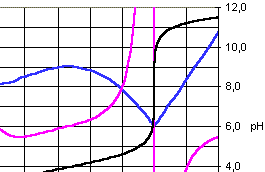
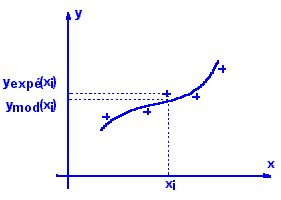
| La valeur de la dérivée
peut en première approximation être estimée par
le taux d'accroissement de cette grandeur (approximation linéaire). Dans le cas de données bruitées, on obtiendra une meilleure estimation de la valeur de la dérivée en approximant la portion de courbe grandeur = f(variable) autour du point considéré par un polynôme de degré 1, 2 ou 3 puis en calculant la valeur de la dérivée de ce polynôme au point considéré. C'est cette méthode qui est utilisée par le tableur REGRESSI. |
|||
| Cours (fichiers
PDF) |
Exercices (fichiers Excel ® ) | ||
 |
Dérivation numérique
(199 ko) |
Exercices
1 à 7 (98 ko) |
|
|
|
|||
|
|||
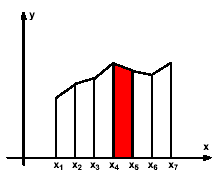
| L’intégration numérique ne pose pas de problème particulier. | |||
| Cours (fichiers PDF) |
Exercices (fichiers Excel ® ) | ||
 |
Intégration numérique (125 ko) |
Exercices 1, 2, 3 (50 ko) |
|
|
|
|||
|
|||
Après
une étude des régressions polynomiales  ,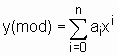
linéaires par rapport aux paramètres ai, l'utilisation du
solveur d'EXCEL permet d’optimiser les paramètres dans le cas de
modèles non linéaires par rapport aux paramètres. Dans tous les cas, on
minimise la critère quadratique  .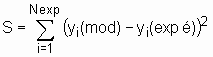
|
|||
| Cours (fichiers PDF) |
Exercices (fichiers Excel ® ) | ||
 |
Modélisation (180 ko) Régression linéaire Régression polynomiale |
Exercices 1 à 8 (120 ko) |
|
