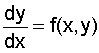
A partir de la connaissance de la valeur de y = y0 pour une valeur de x = x0,
on peut calculer la valeur de
La valeur estimée de y pour x = x0 + dX sera prise égale à
Appelons h le pas d’intégration :
Résolution numérique d'une équation différentielle
Méthode
d’EULER
Cas d’une équation différentielle du premier ordre dont la forme mathématique
est : 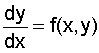
A partir de la connaissance de la valeur de y = y0
pour une valeur de x = x0,
on peut calculer la valeur de ![]() en ce point,
soit
en ce point,
soit ![]() .
.
La valeur
estimée de y pour x = x0 + dX sera prise égale
à ![]() .
.
Appelons h le pas d’intégration :
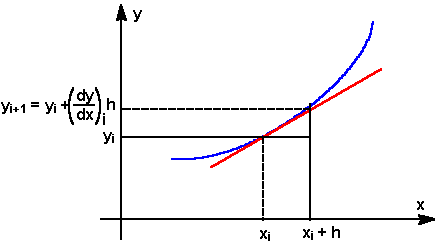
La courbe en trait plein correspond à la solution analytique.
Exemple mathématique
Considérons l'équation différentielle :![]() avec y(x=0)=1
avec y(x=0)=1
La solution analytique est : ![]()
|
i |
xi |
|
|
0 |
0 |
1 |
|
1 |
0,1 |
0,9900 |
|
2 |
0,2 |
0,9608 |
|
3 |
0,3 |
0,9139 |
|
4 |
0,4 |
0,8521 |
|
5 |
0,5 |
0,7788 |
Méthode d'EULER : à compléter ligne par ligne
|
i |
xi |
yi |
Dy = -2 ´ xi ´ yi ´Dx |
Yi+1= yi +Dy |
|
0 |
0 |
1 |
-2´0´1´0,2 = 0 |
1 |
|
1 |
0,2 |
1 |
-2´0,2´1´0,2 = - 0,08 |
0,92 |
|
2 |
0,4 |
0,92 |
-2´0,4´0,92´0,2 = - 0,15 |
0,77 |
|
3 |
0,6 |
0,77 |
||
|
4 |
0,8 |
|||
|
5 |
1,0 |
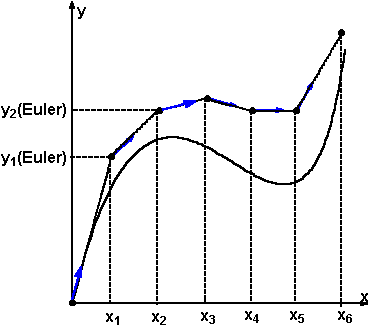
L’exemple ci-dessous montre que la méthode d’EULER pourrait être mise en œuvre « à la main ».
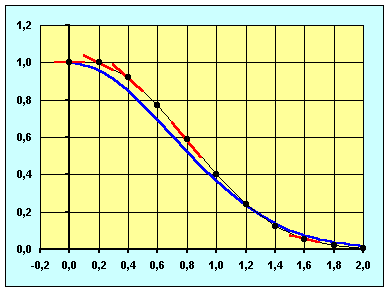
La courbe en trait gras correspond à la solution exacte,
les points correspondent aux valeurs obtenues par la méthode d’EULER.
Le principe
de la méthode d’EULER est rappelé par les segments.
Décharge d’un condensateur dans une résistance.
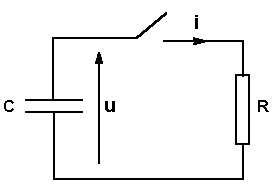
![]()
![]()
Solution
analytique : ![]() Méthode
d’EULER :
Méthode
d’EULER : ![]()
|
A |
B |
C |
D |
|
|
t |
u(Exact) |
u(Euler) |
Du |
|
|
7 |
0 |
=U0*EXP(-t/RC) |
5 |
=dt*(-1/RC)*C7 |
|
8 |
=A7+dt |
=U0*EXP(-t/RC) |
=C7+D7 |
=dt*(-1/RC)*C8 |
|
9 |
=A8+dt |
=U0*EXP(-t/RC) |
=C8+D8 |
=dt*(-1/RC)*C9 |
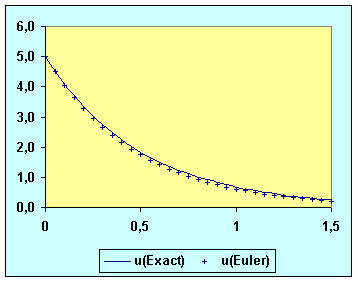
Résultats obtenus :
|
dt |
0,05 |
s |
|
RC |
0,5 |
s |
|
U0 |
5 |
V |
Oscillations amorties

![]() soit
soit ![]()
On pose : ![]() L'équation ci-dessus
devient :
L'équation ci-dessus
devient : ![]()
On a donc transformé l’équation différentielle du 2ème
ordre en 2 équations différentielles du premier ordre :
·
![]() à partir de
laquelle on obtient
à partir de
laquelle on obtient ![]()
On calcule de proche en proche les valeurs de la vitesse
à partir des valeurs de v(t=0) et x(t=0).
·
![]() à partir de
laquelle on obtient :
à partir de
laquelle on obtient :![]() .
.
On calcule de proche en proche les valeurs de x(t) à
partir de la valeur de x(t=0) et des valeurs de v(t) déterminées précédemment.
Remarque : lorsque l’on entreprend
le calcul de x(t+dt),on connaît déjà la valeur de v(t+dt).
Pour calculer v(t+dt),
on peut utiliser ![]() ou
mieux
ou
mieux ![]()
![]() Solutions analytiques :
Solutions analytiques :
SI (a2- w02)
< 0 : 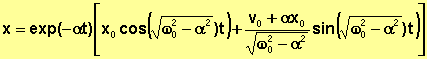
SI (a2- w02)
= 0 : ![]()
SI (a2- w02)
> 0 : 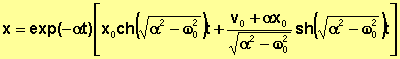
|
dt |
w02 |
a |
x0 |
v0 |
|
0,02 |
50 |
1 |
0,05 |
0 |
|
s |
s-2 |
s-1 |
m |
m.s-1 |
|
A |
B |
C |
D |
E |
|
|
t |
V |
DV |
X(Euler) |
DX |
|
|
0 |
=v0 |
=(- w02*D30-2*a*B30)*dt |
=x0 |
=V*dt |
|
|
31 |
=A30+dt |
=B30+C30 |
=(- w02*D31-2*a*B31)*dt |
=D30+E31 |
=V*dt |
|
32 |
=A31+dt |
=B31+C31 |
=(- w02*D32-2*a*B32)*dt |
=D31+E32 |
=V*dt |
|
33 |
=A32+dt |
=B32+C32 |
=(- w02*D33-2*a*B33)*dt |
=D32+E33 |
=V*dt |
|
34 |
=A33+dt |
=B33+C33 |
=(- w02*D34-2*a*B34)*dt |
=D33+E34 |
=V*dt |
Etude les différents régimes :
|
Régime pseudo-périodique a2 - w02 < 0 y(0)
= 0,05 m |
|
|
Régime critique a2
- w02 = 0 Le retour à l'équilibre s'effectue plus rapidement que dans le régime apériodique |
|
|
Régime apériodique a2
- w02 > 0 |
|
Chute libre
![]()
|
|
Solution exacte : y=0,5´g´t2+v0´t+y0 |
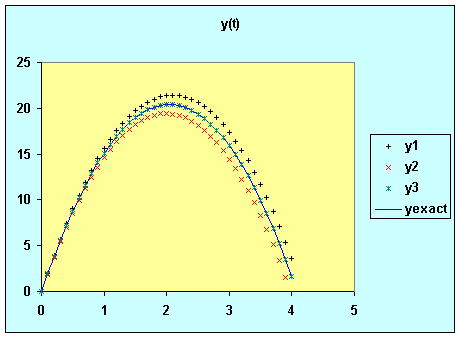 y(t)
y(t)
|
y0 |
v0 |
g |
dt |
|
0 |
20,0 |
9,80 |
0,10 |
|
m |
m.s-1 |
m.s-2 |
s |
Cet exemple
met en évidence l’intérêt du choix de la méthode (3) :
![]()
Chute amortie par des forces de frottement pouvant être modélisée par -kV2
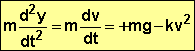 ou
ou 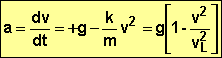 ,
,
VL désignant
la vitesse limite atteinte par l’objet.
Si on
tient compte de la poussée d’Archimède, g’ < g.
Résolution analytique |
· Expression de v(t)
Effectuons les changements de variable : v = u vL et
![]() avec
avec ![]()
![]() ou
ou
![]()
Une primitive de ![]() est de la forme :
est de la forme : ![]()
Conditions initiales : t=0 Û x=0
et v=v0 Û
u0=v0/vL
On obtient ![]() soit
soit ![]()
dont on déduit : 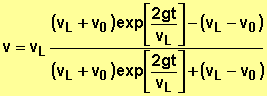
Si v = v0 = 0
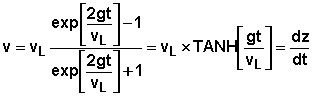
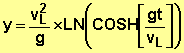
· Expression de v(y)
![]() soit
soit
![]()
On pose ![]()
On obtient l’équation
différentielle : ![]()
La solution qui vérifie
les conditions initiales est : 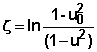
ou
![]()
En revenant aux variables
initiales : 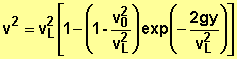
Résolution numérique |
|
|
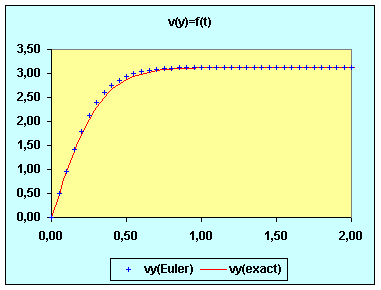
La détermination des valeurs de y(t) peut se faire par une des trois méthodes suivantes :
|
Résultats de la résolution numérique :
|
dt |
0,05 |
s |
B=k/m |
1,00 |
m-1 |
|
|
g |
10,00 |
m.s-2 |
vy0 |
0,00 |
m.s-1 |
|
B |
C |
D |
E |
F |
|
|
t |
DVy |
Vy |
Dy |
y |
|
|
10 |
0 |
=(g-B*Vy^2)xdt |
0 |
=Vy*dt |
0 |
|
11 |
=B10+dt |
=(g-B*Vy^2)*dt |
=D10+C10*dt |
=Vy*dt |
=F10+E10 |
|
12 |
=B11+dt |
=(g-B*Vy^2)*dt |
=D11+C11*dt |
=Vy*dt |
=F11+E11 |
Page d'accueil Méthodes numériques Méthode d'EULER Ressources TS