Histoire de la Cryptographie
L'Homme a toujours eu un besoin fondamental de communiquer.
Lorsqu'il a eu besoin de dissimuler les informations qu'il souhaite communiquer à une personne en particulier il a inventé des techniques qui lui permettent de rendre les messages incompréhenssibles pour
les personnes qui peuvent eventuellement les intercepter ou les transporter.
La cryptographie est l'ensemble des techniques qui permettent de chiffrer un message pour le transmettre sans le dissimuler lors de son transport. Ces techniques ont été vaincues au cours de l'histoire par des cryptanalystes.
La cryptanalyse est la discipline inverse de la cryptographie qui consiste à retrouver les messages chiffrés sans connaître la clef ou la méthode de leurs chiffrement. Ces deux disciplines réunies composent la cryptologie
La cryptologie a évoluée au cours du temps en en fonction de l'évolution des sciences et des technologies.
La cryptographie est l'ensemble des techniques qui permettent de chiffrer un message pour le transmettre sans le dissimuler lors de son transport. Ces techniques ont été vaincues au cours de l'histoire par des cryptanalystes.
La cryptanalyse est la discipline inverse de la cryptographie qui consiste à retrouver les messages chiffrés sans connaître la clef ou la méthode de leurs chiffrement. Ces deux disciplines réunies composent la cryptologie
La cryptologie a évoluée au cours du temps en en fonction de l'évolution des sciences et des technologies.
La scytale spartiate
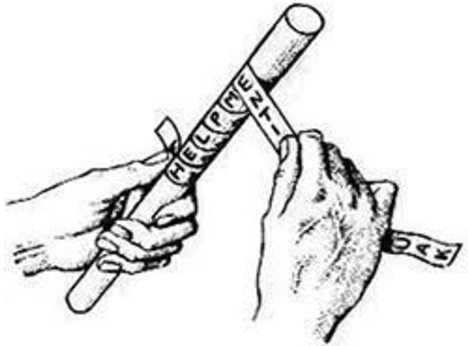utilisé par les spartiates à usage militaire dès le Vème siècle avant JC. Elle consiste en 2 bâtons ronds, parfaitement égaux en longueur et en grosseur.
Les 2 personnes qui communiquent à l'aide de ce système ont chacun un bâton.
l'emetteur du message enroule une bande de parchemin, longue et étroite, autour de sa scytale, sans laisser d'intervalle entre les bords de la bande. Il écrit sur ce parchemin le
message qu'il veut transmettre puis enlève la bande et l'envoi au destinataire. Le transporteur du message ainsi que toute personne qui intercepterait la bande, n'y lira que des
caractères qui forment des mots sans aucun sens. Le distinataire, qui possède une scytale identique en tout point à celle de l'emetteur, pourra déchiffrer le message en enroulant la
bande autour de sa scytale comme l'a fait l'émetteur.
Faiblesse
Lorsque l'on sait que le texte a été chiffré avec la scytale, on peut essayer de lire une lettre sur deux, sur trois, sur quatre, jusqu'à ce que le texte prenne sens : cela revient à essayer les “n” possibilités. Il s'agit d'une attaque par force brute qu'il est facile de réaliser.Le carré de Polybe
Inventé aux environs de 150 avant J-C en Grèce. C'est le premier système de chiffrement par substitution monoalphabétique connu.
Ce système composé d'un carré de 25 cases dans lesquelles sont placées les lettres de l'alphabet (w est mis dans la même case que v). Chaque lettre est représentée par ses coordonnées
dans ce carré : d'abord le numéro de sa ligne puis celui de sa colonne.
Plusieurs variantes sont possibles, par exemple avec un carré de 6 x 6 on peut ajouter les chiffres 0 à 9 en plus de toutes les lettres de l'alphabet français.
Faiblesse
Il est facile de briser ce chiffrement par analyse des fréquences car une lettre est toujours remplacée par la même combinaison de chiffres.Le Chiffrement par décalage
Aussi connu comme le chiffre de César ou le code de César, Il fut utilisé, si ce n'est inventé, par Jules César lors de la Guerre des Gaules pour rendres les messages envoyés
aux géneraux incompréhensibles s'ils étaient interceptés par l'ennemi.
le principe de ce mode de chiffrement consiste à décaler les lettres de l'alphabet d'une certaine valeur vers la droite ou vers la gauche. Cette valeur est la clé de chiffrement
Faiblesse
il n'y a que 25 façons différentes de chiffrer un message, cela en fait donc un code très peu sûr et facile à casser par une attaque par force brute. Il est aussi vulnérable à l'analyse des fréquences qui s'appui sur le nombre de fois qu'une lettre de l'alphabet revient dans un texte. Malgré ces faiblesses et en raison de sa grande simplicité, le code de César fut encore employé par les officiers Sudistes pendant la guerre de Sécession, et même par l'armée russe en 1915.Le cadran d'Alberti
Pour remédier à la faiblesse de la cryptographie par substitution monoalphabétique, Leon Battista Alberti inventa, vers 1460, le premier procédé de chiffrement polyalphabétique appelé
disque d'Alberti. Deux disques concentriques. Sur le plus grand, fixe, sont écrites les lettres de l'alphabet les plus utilisées dans le bon ordre (sans les lettres J, H, K, U, W et Y)
ainsi que les chiffres 1, 2, 3 et 4. Sur le plus petit, mobile, sont écrites dans le désordre, les lettres de l'alphabet (sans le j et le w).
Pour chiffrer un message, l'émetteur :
- Choisit une lettre une lettre index sur le disque fixe (par exemple 'A')
- Choisit une lettre au hasard sur le disque mobile et la place sous la lettre choisie comme index puis maintenant les 2 disques dans cette position
- Ecrit, en minuscule, la lettre choisit au hasard au début du message crypté.
- Lit sur le disque mobile une lettre du message clair et la remplace par celle du disque fixe située juste au dessus.
- Ecrit chaque lettre ainsi cryptée, en majuscule, à la suite du message crypté.
- Après avoir chiffré quelques lettres, il place une autre lettre du disque mobile sous la lettre choisie comme index et recommence les étapes 3 à 6 jusqu'à avoir crypté toutes les lettres du message clair
- disposer d'un cadran identique à celui de l'émetteur
- connaitre la lettre qui a été choisie, par l'émetteur, comme index
- savoir que les minuscules ne sont pas des caractères correspondant à une lettre claire, mais des lettres qui indiquent que l'on doit tourner le le disque mobile en alignant cette lettre avec la lettre choisie comme index.
Faiblesse
Le chiffrement de Vigenère
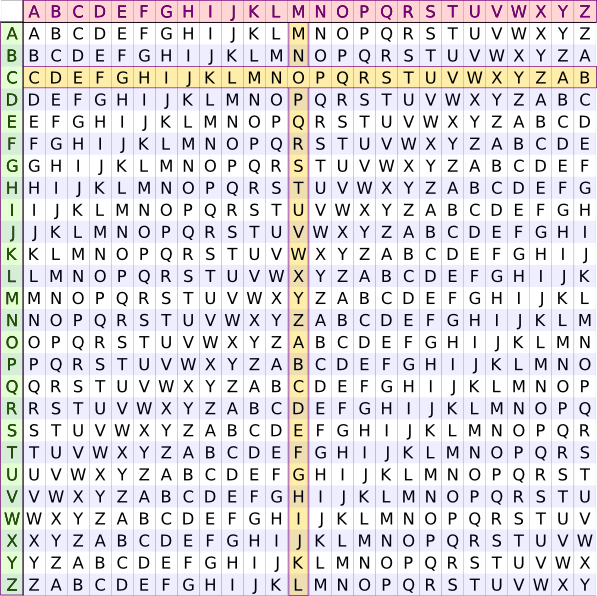Concu par le cryptographe francais Blaise de Vigenère en 1586, c'est un système de chiffrement par substitution polyalphabétique dans lequel une même lettre du message clair peut,
suivant sa position dans celui-ci, être remplacée par des lettres différentes, contrairement à un système de chiffrement mono alphabétique comme le chiffre de César (qu'il utilise
cependant comme composant).
Ce procédé de chiffrement utilise une clé de cryptage (mot de longueur arbitraire) et une table carrée (auant de lignes que de colonnes), composée de 26 caractères de l'alphabets écrits dans l'ordre et décalés de ligne en ligne d'un caractère. La tête de cololonnes de cette table (ligne tout en haut) contient un alphabet complet, pour la clé, et à gauche, verticalement (tête de lignes), un alphabet, pour le texte à coder.
L'emetteur et le destinataire du message disposent de la même table et de la même clé de cryptage
Pour chiffrer un message : on choisit une clé. On écrit ensuite cette clé sous le message à coder, en la répétant autant de fois que nécessaire pour que, sous chaque lettre du message à coder, on trouve une lettre de la clé. Pour coder, on regarde dans le tableau l'intersection de la ligne de la lettre à coder avec la colonne de la lettre de la clé.
pour déchiffrer un message : il suffit de rechercher la lettre du message codé dans la colonne de la lettre de la clé et de lire la lettre du texte clair dans la colonne qui represente la tête de ligne de la table.
Faiblesse
Le cryptage ADFGVX 1ère Guerre Mondiale
De 1914 à 1918 les chiffrements n'ont que peu progressé et la plupart d'entre eux ne vécurent que le temps de les déchiffrer. On peut noter l'un des plus fameux, le code ADFGVX,
un système de chiffrement allemand inventé par le lieutenant Fritz Nebel en 1918. le lieutenant francais Georges Painvin réussit à casser ce code et à décrypter le code ennemi
éclairant ainsi les Français sur tous les agissements allemands.
La mise en place de ce dispositif se fait en 2 étapes :
Première étape : On utilise une grille de taille 6x6 remplie des 26 lettres de l'alphabet et des 10 chiffres. Les lignes et les colonnes sont indexées par les lettres ADFGVX. Pour chiffrer un message, on note uniquement la lettre correspondant à la ligne et celle correspondant à la colonne (un peu comme dans le carré de Polybe). A ce stade, c'est une simple substitution monoalphabétique, et l'analyse des fréquences en viendrait à bout facilement. C'est pour cela qu'une seconde étape est utilisée.
Seconde étape : On choisit clé (un mot) secret et connu uniquement des deux correspondants et on crée un tableau avec autant de colonnes que la longueur de la clef et on place la les lettres de la clé en têtes de colonnes. On inscrit ensuite le message à chiffrer avec un caractère par colonne, sur plusieurs lignes.Enfin on permute les colonnes de la table de telle sorte que les lettres de la clé soient rangées dans l'ordre alphabétique. Le lettres lues dans cette dernière table ligne par ligne constituent le message crypté.
Faiblesse
La machine Enigma 2ème Guerre Mondiale
Enigma est la première méthode de cryptographie électronique. Elle a été utilisée par les armées allemandes du début des années trente jusqu'à la fin de Seconde Guerre Mondiale.
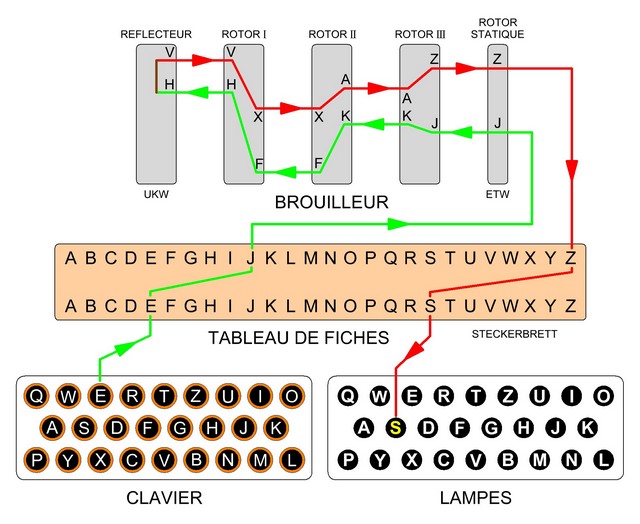
Cette machine ressemble à une machine à écrire. Quand on presse sur une touche, une lettre s'allume sur un panneau lumineux: c'est la lettre chiffrée. Puis, un mécanisme fait tourner le rotor de droite d'un cran; toutes les 26 frappes, le deuxième rotor tourne d'un cran, toutes les 676 frappes, c'est le troisième rotor qui tourne d'un cran. Certaines Enigmas avaient 3 rotors, d'autres en avaient 4 ou 5. Ces rotors tournants modifient les connexions électriques dans la machine, ce qui fait que la touche "A" allumera peut-être le "B" la première fois, mais le "X" la deuxième, le "E" la troisième, etc.
C'est le nombre faramineux de réglages de la machine qui fait sa force et ces réglages changeaient évidemment chaque jour. On peut en effet changer l'ordre des rotors,leur orientation initiale et les branchement du tableau de connexions. Par exemple, on pouvait spécifier la clef du jour ainsi:
Position des rotors : 2 - 3 - 1
Orientations des rotors : 2 - 23 - 5
Branchements des connexions : A/L - P/R - T/D - B/W - K/F - O/Y
Indicateurs : B - W - E
Au final, on a:
26 x 26 x 26 = 17'576 combinaisons liées à l'orientation des chacun des trois rotors,
6 combinaisons possibles liées à l'ordre dans lequel sont disposés les rotors,
100'391'791'500 branchements possibles quand on relie les six paires de lettres dans le tableau de connexions.
Les machines Enigma à 3 rotors peuvent donc chiffrer un texte selon 17'576 x 6 x 100'391'791'500 = 10'000'000'000'000'000 combinaisons différentes!
