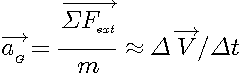
La m�thode d'Euler
Il s'agit certainement de la
m�thode la plus simple d'int�gration num�rique.
Elle permet d'atteindre une pr�vision correcte des r�sultats exp�rimentaux si
le pas de r�solution est � suffisamment � petit.
Elle permet une pr�vision de l'�volution, en fonction du temps, de la vitesse et
de la position d'un mobile.
On ne consid�rera que des mouvements de translation
rectiligne.
Apr�s un bilan des forces ext�rieures s'exer�ant sur le mobile,
l'acc�l�ration est obtenue � partir de :
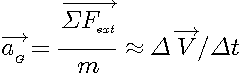
|
Il faut comprendre qu'entre deux
lignes cons�cutives,
|
Aussi est-il n�cessaire de choisir des
incr�mentations les plus petites possibles pour t, d'o� un nombre de calculs
longs et fastidieux ...
L'utilisation d'un tableur s'impose.
|
EXEMPLES |
COMMENTAIRES |
|
Il permet de montrer
l'influence du pas sur les r�sultats obtenus |
|
|
Mouvement sinuso�dal amorti par des
frottements fluides du type : |
|
|
Mouvement de chute avec frottements |
R�solution num�rique
d'une �quation diff�rentielle dont la solution analytique |
![]() Page d'accueil
Pages Physique M�thodes
num�riques Nouveaux
programmes TS
Page d'accueil
Pages Physique M�thodes
num�riques Nouveaux
programmes TS